اخيلس بطل الأبطال محارب بلاد اليونان الأول وقاهر الطرواديين. خلد هوميروس اسمه فجعله نجم الياذته.  عمدته امه بعد ولادته حسب الأسطورة اليونانية القديمة  فى احد أنهار العالم السفلى فغمرت المياة جميع اجزاء جسمه باستثناء كعبه لأن امه كانت تمسكه منه.  فاصبح جسده لا يقهر باستثناء كعبه اللذى اصبح نقطة ضعفه!

فاذا اردنا أن نذكر اخيلس فلا بد ان نروى الحقيقة  كاملة كما هي. فلا نبخسه حقه فى فى التأكيد على قوته و براعته. لكن فى  الوقت نفسه لا ينبغي ان نبالغ ونغض الطرف عن عيوبه ونقاط ضعفه. هذا هو الطرح العلمى لأى موضوع.

و كذلك الأمر بالنسبة للهندسة الاقليدية. فقد اكتسبت عبر القرون و الالفيات المتعاقبة سمعة اكثر من رائعة. فهى اية من أيات الجمال والدقة و الكمال. فالهندسة الاقليدية لا تقل فى جمالها عن أرقى الأداب كما ان تجاربنا الحياتية أكدت دقتها بدرجة مذهلة و كل اجزائها تكمل بعضها بدون زيادة أو نقصان. هذا كله اكسب الهندسة الاقليدية هالة من القداسة. بل واعتبرها البعض فى العصور الوسطى برهان على الأعجاز الألهي وانها تعكس الأسلوب الألهي فى خلق الكون. فاى تشكيك فيها يعتبر  نوع من الألحاد والكفر بالدين.

ونحن لا نقصد من عنوان اليوم ان هندسة اقليدس خاطئة او معيبة. لكنها محاولة للطرح العلمى و التحليل الرياضى لهذا الفن الأقليدي. وكما نعلم فان اقليدس قد بنى هندسته على 23 تعريفا و5 بديهيات و 5 مسلمات. وبقدر صحة هذه الأوليات تكون سلامة الهندسة الأقليدية كلها. ومايهمنا اليوم هى المسلمات الخمسة وبخاصة الاخيرة منها. فدعونا نستعرض اولا هذه المسلمات.

المسلمات الخمسة Postulates :
1 بين كل نقطتين مختلفتين يمكننا توصيل خط مستقيم -وحيد-
2 يمكننا مد اى قطعة مستقيمة من كلا طرفيها الى مالا نهاية
3 يمكننا رسم اى دائرة اذا علمنا مركزها ونصف قطرها
4 جميع الزوايا القائمة متساوية
5 اذا قطع مستقيمان ثالث بحيث يكون مجموع الزاويتين  الداخليتين على جهة واحدة من القاطع اقل من قائمتين. فان المستقيمان سوف يلتقيان اذا مددناهما على نفس هذه الجهة.

أما المسلمة الاولى فهي توضح طبيعة الخط المستقيم من وجهة النظر الأقليدية. و المسلمتان الثانية و الثالثة تفيدان بان المكان ممتد و لانهائى بدون فجوات أو مناطق خارج نطاق سيطرة الهندسة الأقليدية. و المسلمة الرابعة قد تبدو غريبة للوهلة الأولي ولكنها تتناسب مع هدف اقليدس الأصلي لدارسة خواص الاجساد الجاسئة عند ازاحتها فى المكان. وهي تفيد فى الوقت نفسه  بان المكان متجانس homogeneous واتجاهاته متماثلة isotorpy . اما المسلمة الخامسة فهى الفارق الرئيس بين هندسة اقليدس وسواها. ودعونا نستعرضها بشئ من التفصيل.

المسلمة الخامسة

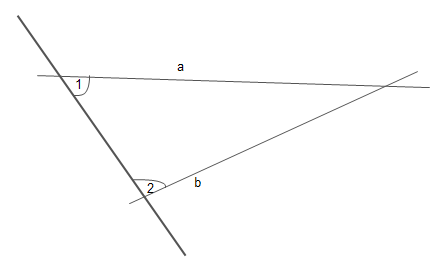
تفيد المسلمة الخامسة أنه اذا قطع  خطان a و b كما فى الرسم خطا ثالثا بحيث يكون مجموع الزاويتين الداخليتين جهة اليمين اقل من 180 درجة -أو قائمتين كما هي لغة اقليدس- فاننا اذا مددنا الخطان على استقامتهما جهة اليمين فلا بد  ان يتقاطعا .

قد يلفت نظرنا ان صياغة هذه المسلمة طويلة وتحتوى على جمل اكثر.واننا نحتاج الى التركيز اكثر حين قراءتها مقارنة بالمسلمات السابقة. ولذلك ظهر التساؤل:  لماذا هذه المسلمة اطول؟ الا يمكن صياغتها بصورة اقصر؟ هل هذه المسلمة مستقلة عن سابقاتها؟ ام انه يمكن برهنتها بدلالة المسلمات السابقة؟

فى الحقيقة توجد صياغة حديثة للمسلمة الخامسة أقصر وهى صياغة مهمة وتعرف بصياغة بلايفير Playfair وتقول هذه الصياغة:
” اذا كان لدينا خط مستقيم ولدينا نقطة خارجه فابمكاننا رسم مستقيم وحيد يمر بهذه النقطة بحيث يكون موازيا للمستقيم الاول”

وهاتان الصياغتان تبدوان للوهلة الأولى مختلفتين تماما. ولبرهنة كيف ان صياغة بلايفير مكافئة لصياغة اقليدس الاصلية يمكننا تقديم البرهان التالى:

صياغة بلافير

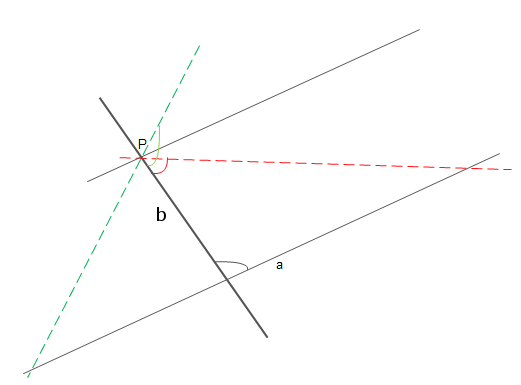
اذا كان لدينا خط مستقيم a و نقطة P تقع خارجه. كخطوة مساعدة ننشأ اولا الخط b اللذي يمر ب P ويقطع المستقيم  a.  ثم من P نرسم خطا جديدا وهذا ذو 3 أحتمالات:
1 أن يكون مجموع الزاويتن الداخليتين جهة اليمين اقل من قائمتين او 180 درجة كالخط الأحمر. اذن سيتقاطع الخطان على الجهة اليمني.
2 أن يكون مجموع الزاويتين جهة اليمين اكبر من 180 درجة كالخط الأخضر. وبما ان تعريف اقليدس العاشر يقول أن الزاوية المستقيمة تساوي قائمتين او 180 درجة. اذن سوف يكون مجموع الزاويتين الداخليتين جهة اليسار اقل من 180 درجة وسوف يتقاطع الخطان جهة اليسار
3 أن يكون مجموع الزاويتين الداخليتين جهة اليمين يساوى 180 درجة تماما. اذن لن يتقاطع الخطان جهة اليمين. كما أن مجموع الزاويتين الداخليتين جهة اليسار سيساوى ايضا 180 درجة . اذن فلن يتقاطع الخطان جهة اليسار وسنحصل كما فى تعريف اقليدس الثالث و العشرين على خطين متوازيين!
ومن هنا نرى انه بامكاننا ان نرسم خط مواز للمستقيم الاول فى حالة واحدة فقط.  وهو ان يكون مجموع الزاويتين الداخليتين 180 درجة تماما!

لكن ما تأثير المسلمة الخامسة على الهندسة الاقليدية. وماذا سوف يحدث اذا استغنينا عنها؟ هل لن يتغير الكثير؟ هل هي مجرد كلام رياضيين بيروقراطيين متحذلقين لا يغير كثيرا من الواقع القائم؟ دعونا نرى.

الزوايا المتناظرة و المتبادلة

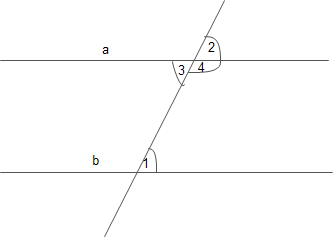
نعلم من دراستنا المدرسية انه اذا قطع خطين متوازيين خط ثالث تكون الزوايا المتناظرة و المتبادلة متساوية. كما فى الرسم فالخطان a و b متوازيان قطعهما خط ثالث فتكون الزاويتان 1 و 2 متساويتين بالتناظر و الزاويتان 1 و 3 متساويتين بالتبادل. لكن من أين أتت هذه النتيجة؟ انها اتت من المسلمة الخامسة. كيف؟

حيث ان الخطين a و b متوازيان اذن يكون مجموع الزاويتين الداخليتين 1 و 4 يساوي 180 درجة كما اوضحنا سلفا. ونلاحظ ايضا ان مجموع الزاويتين 4 و2 يساوي 180 درجة لانهما يصنعان زاوية مستقيمة. اذن كلا من الزاويتين 1 و2 تكملان نفس الزاوية 4 اذن فهما متساويتان. وهما زاويتان متناظرتان!  وبالمثل فان الزاوية 3 تكمل الزاوية 4 لانهما يصنعان خطا مستقيما. وكما سبق فان الزاويتين 1 و 4 مجموعهما 180 درجة. اذن الزاوية 1 تساوى 3 وهما زاويتان متبادلتا!.

اذن اذا استغنينا عن المسلمة الخامسة  فسوف نفقد القاعدة اللتى تفيد تساوى الزوايا المتناظرة و المتبادلة! ربما تكون هذه مفاجئة غير مريحة قليلا. لكن هذا ليس كل شئ. فالمسلمة الخامسة تلعب دورا اكبر فى الهندسة الاقليدية!

نعلم ان مجموع زوايا المثلث الداخلية 180 درجة. لكن من اين اتت هذه النظرية؟ مرة اخرى انها اتت من المسلمة الخامسة. كيف؟

مجموع زوايا المثلث الداخلية يساوي 180 درجة

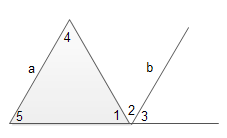
كما فى الرسم لدينا مثلث زواياه الداخلية هى 1 و 4 و 5 . كخطوة مساعدة نرسم الخط b يوازي a وكما رأينا سلفا فان الزاويتين 2 و 4 متبادلتان اذن فهما متساويتان. كما ان الزاويتين 3 و 5 متناظرتان اذن فهما متساويتان. وحيث ان مجموع الزاويا 1 و 2 و3 يساوى قائمتين او 180 درجة لانهم يصنعون خطا مستقيما اذن مجموع الزويا 1 و 4 و5 هو 180 درجة ايضا. وهو المطلوب اثباته. اذن اذا تخلينا عن المسلمة الخامسة فلن يكون مجموع زوايا المثلث 180 درجة!

مما لا شك فيه ان خسارتنا هذه المرة اكبر. لان نظرية مجموع زوايا المثلث الداخلية نحتاج اليها كثيرا خصوصا فى مسائل التشابه و التطابق. فاذا كان لدينا مثلثان فيهما زاويتان متساويتان فان هذا يكفينا لان نصل الى ان الزاوية الثالثة فى المثلث الأول تساوى الزاوية الثالثة فى الثانى. لانهما تكملان  الزوايا المتساوية السابقة.

وليس هذ كل شئ يتعلق بالمسلمة الخامسة. فهناك مفاهيم اساسية تتوقف عليها. مثلا المربع. ماهو  المربع؟ طبقا لتعريف اقليدس هو شكل رباعى الاضلاع كل اضلاعه متساوية وكل زواياه قائمة. لكن ما هو الدليل ان المربع شكل ممكن هندسيا؟ وكيف نبرهن ان المربع ممكن انشاؤه رياضيا؟ مرة اخرى دعونا نبحث عن البرهان!

انشاء مربع

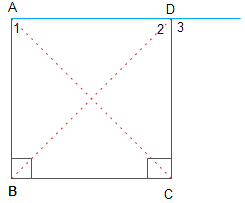
نرسم اولا القطعة المستقيمة BC بطول 5 سم ثم نقيم من B و C عمودين  -AB و DC- على BC  بطول 5 سم على نفس الجهة. الأن نصل الضلع AD . كيف نستطيع الان ان نبرهن ان AD طوله 5سم؟ وأن الزاويتين 1 و 2 قائمتان؟ دعونا نستخدم لذلك حالات التطابق. المثلثان ABC و BCD متطابقان بدلالة ضلعين وزاوية محصورة. حيث أن:
1 BC ضلع مشترك
2 الضلعان AB و CD  متساويان ويساويان 5 سم
3 الزاويتان B و C قائمتان
ينتج من التطابق ان الضلعين AC و BD متساويان.
ثم بتطابق المثلثين BAD و ADC بدلالة 3 أضلاع هي:
1 AD ضلع مشترك
2 الضلعان AB و CD  متساويان ويساويان 5 سم
3 الضلعان AC و BD متساويان كما برهنا سلفا
ينتج من التطابق ان الزاوية 1 تساوى الزاوية 2. وهذه نتيجة هامة.وكنا نريد الوصول اليها. ولكننا لم نثبت بعد انهما يساويان 90 درجة. اذن كيف يمكننا ان نبرهن ان الزاويتين هما ايضا قائمتان؟ لذلك نحتاج نظرية التوازي. فحيث ان مجموع الزاويتين الداخليتين C و B  يساوى 180 درجة اذن AB يوازي DC . ومن ثم فان الزاوية 1 تساوى الزاوية 3 بالتناظر. اذن الزاوية 2 تساوى الزاوية 3 ايضا وحيث ان مجموعهما 180 درجة. اذن كل من الزوايا 1 و 2 و 3 يساوى 90 درجة! ولكننا كما نرى قد استخدمنا مرة اخرى المسلمة الخامسة! فبدونها لا يوجد مربع او مستطيل طبقا للتعريف الاقليدي!

مثال اخير يتعلق باشهر نظرية هندسية ارتبط اسمها باسم علم وهى نظرية فيثاغورث. فحتى هذه النظرية سوف تسقط بسقوط المسلمة الخامسة!  ماذا تقول نظرية فيثاغورث؟ انها تقول ان مربع وتر المثلث القائم الزاوية يساوى مجموع مربعى ضلعى القائمة. لكن ما هو البرهان على ذلك؟ اذا بحث الانسان فى شبكة الانترنت عن برهان لهذه النظرية فسيجد براهين مختلفة. ولكنها كلها اما تعتمد على انشاء مربعات او ان مجموع الزاويا الداخلية لمثلث يساوى 180 درجة. وهذه كلها نتائج تعتمد على  المسلمة الخامسة وتسقط بسقوطها. وعلى سبيل المثال دعونا نرى برهان قصير جميل لنظرية فيثاغورث.

برهان نظرية فيثاغورث

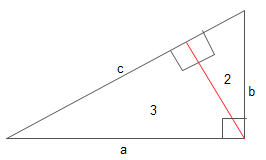
كما فى الرسم لدينا مثلث قائم الزاوية وهو المثلث الكبير وسنطلق عليه المثلث 1. نقيم عمود وهو الخط الأحمر. فنحصل على مثلثين صغيرين هما 2 و 3 وهما ايضا مثلثان قائما الزاوية. ونلاحظ ان المثلثات الثلاثة متشابهة حيث انها تمتلك ثلاث زوايا متساوية. حيث:
1 كل مثلث يحتوى على زواية قائمة
2 هناك دائما زاوية مشتركة بين كل مثلثين مع المثلث الكبير
3 حيث ان مجموع زوايا المثلث الداخلة 180 درجة تكون الزاوية الثالثة متساوية فى كل المثلثات.
من خواص الاشكال المتشابهة ان مساحتها تتناسب مع مربع طول اضلاعها المتناظرة كما ان مساحة المثلث الكبير تساوى مجموع مساحتى المثلثين الصغيرين ومن هنا يمكننا ان نقيم العلاقتين التاليتين مع مراعاة ان A1 تعنى مساحة المثلث 1 و A2 تعنى مساحة المثلث 2 وهكذا. و بفرض ان معامل التناسب بين مساحة المثلث ومربع الضلع هو x:
A1  = A2 + A3
x.c^2 = x.b^2 + x.a^2
بقسمة طرفى المعادلة على x نحصل على
c^2 = a^2 + b^2
وهو المطلوب اثباته. ولكننا كما رأينا استخدمنا لبرهان ذلك نظرية ان مجموع زوايا المثلث الداخلية يساوي 180 درجة.

فى النهاية يمكننا ان نستنتج امرين. الأول هو ان الهندسات الغير اقليدية -اللتى لا تعترف بالمسلمة الخامسة لاقليدس بل وتفرض عكسها كما سنرى فى مرة قادمة- مستقلة تماما عن الهندسة الاقليدية والقول بان الهندسات الغير اقليدية تعتمد فى قلبها على الهندسة الاقليدية هو قول جانبه الصواب. فالهندسات الغير اقليدية عليها أن تشق طريقها بنفسها معتمدة على الاستدلال المنطقى تماما كما فعلت الهندسة الاقليدية. بل ان مهمة الهندسات الغير اقليدية اصعب لان البداهة لا تغطى منطقة عملها. بينما الهندسة الاقليدية قد استفادت كثيرا من البداهة.

الأمر الثانى هو ان الهندسة الاقليدية كلها او جلها تتعلق بخيط المسلمة الخامسة. وهو خيط لا أقول انه واه  ولكنه ان قطع سقطت الهندسة الاقليدية كلها.

اخيلس اننا لن نقتلك -ربما اليوم- لكننا عرفنا اين يوجد مقتلك!