رأينا فى المرتين الماضيتين طريقتين مختلفتين لاجراء عملية الضرب وكان لكلي الطريقتين تعقيد زمنى تربيعي. ورأينا انه اذا زاد طول الأعداد المضروبة ألف مرة مثلا فسيتضاعف الزمن اللازم لاجراء عملية الضرب مليون مرة! ونريد اليوم ان نتعرف على طريقة اخرى لاجراء عملية الضرب تعقيدها الزمنى أفضل من التربيعي.

لكن علينا فى البداية ان نعترف بأن التعقيد الزمنى التربيعى ليس أمرا سيئا فى حد ذاته. فمثلا لو توصل خبراء البرمجة لطريقة ذات تعقيد زمني تربيعى لحل المشكلة المعروفة باسم مشكلة رجل المبيعات salesman problem لكانوا فى قمة السعادة. ومشكلة رجل المبيعات تتعلق بتعيين اقصر مسار يربط بين عدة مدن مختلفة. لكن أهمية ايجاد طريقة كفؤة لاجراء عملية الضرب تعود الي أهمية عملية الضرب في حد ذاتها حيث انها عملية حسابية أساسية. فحضراتكم تقرأون هذا المقال فى صورة رقمية.  ويمكنكم ان تتخيلوا عدد عمليات الضرب اللتى يقوم بها الأن نظام تشغيلكم على الجهاز أمامكم! فأي توفير فى الزمن ولو كان بسيطا فى أجراء عملية الضرب سيكون له فائدة تراكمية عظيمة جدا على كفاءة اجهزة الكمبيوتر فى المجمل.

فى المرة الماضية تعرفنا على طريقة يسميها البعض الطريقة الروسية او طريقة الفلاحين الروس ورأينا انها فى الحقيقة الطريقة المصرية القديمة واليوم سنتعرف على طريقة روسية خالصة. وأن كان لاكتشافها ملابسات غريبة سنعرضها لاحقا.

وتعتمد طريقة اليوم على تقنيتين وأن شئتم فلنقل حيلتين فى منتهى الأهمية والبراعة وفهمهما ضروري لفهم هذه الطريقة. التقنية الاولى تنبع من ميدان البرمجيات وان كانت مستوحاة من الحياة عموما. والتقنية الثانية تنبع من ميدان الرياضيات وهى حيلة بسيطة ولكن فاعلة. فدعونا نتعرف على هاتين التقنيتين.

التقنية الأولي أسمها بالأنجليزية “divide and conquer” وترجمتها الحرفية قسم وأغزو لكن الترجمة الشائعة لها هى “فرق تسد” وفحوى هذه التقنية يذكرنى بموضوع من مواضيع  القراءة فى مادة اللغة العربية مر بي عندما كنت طفلا صغيرا عنوانه على ما أتذكر الأتحاد قوة. ويحكي ان رجلا حكيما جمع ابناءه حول فراشه وأعطاهم حزمة من العصى وطلب منهم أن يكسروها فعجزوا جميعا عن ذلك. هنا أستل الرجل عصا تلو الأخرى واخذ يعطيها لأحد ابنائه ويطلب منه ان يكسرها ففعل ذلك بكل سهولة. وهنا أتت رسالة الرجل الختامية لابنائه: انتم مثل هذه الحزمة مادمتهم متحدين فلا يمكن كسركم. اما اذا صرتم متفرقين فمن السهولة التغلب عليكم. ففي الأتحاد قوة وفى التفرق ضعف.

وهذه القصة تعكس بالضبط فحوى تقنية “فرق تسد” ولكننا هنا نقف على الجانب الأخر من الساحة. فنحن نريد كسر العصى ولذلك من الحكمة ان نتعامل معها بصورة فردية. بل أذا كان كسر العصى يحتاج الى قدرة تربيعة. بمعنى ان كان كسر عصاتين يحتاج لاربعة اضعاف القدرة لكسر عصا واحدة فيصبح عدم تقسيم العصى في هذه الحالة ضربا من ضروب الغباء.

لكن هناك جانبا أخر من جوانب القصة يجب تسليط الضوء عليه لأهميته البالغة. وهو كيف نقوم بعملية التفرقة والتقسيم . فى حالة العصى فالأمر سهل فالعصى هى جمادات لاحول ولا قوة لها نستطيع ان نفرقها بمنتهى السهولة. لكن كيف يفعل ذلك المرء مع اعدائه مثلا؟ هل يقول لهم تعالوا أحاربكم الواحد تلو ألأخر فيردون عليه سمعا وطاعة سنلبى فورا! بالطبع لا. لا يمكن ان يحدث الأمر على هذه الصورة. بل لا بد من خدعة وحيلة ما لتفريق الخصوم. لكن هذه الحيلة ليست دائما مجانية. بل أن لها فى أغلب الاحوال تكلفة ما. وهنا يجب ان نحسب تلك التكلفة ونري هل مازلت مقبولة بالنسبه لتحقيق الهدف الأصلي أم لا. ولا نكن كفرق كرة القدم اللتى تسرف فى المراواغات والحيل وتنسى ان الهدف هو كسب المباريات فلا تستطيع أن تحقق أى نجاح يذكر.

دعوني افرض مثالا خياليا. دعونا نتخيل ان هناك تنينا نريد ان نتغلب عليه. ونكيد له بحيلة. وحيث أننا نعلم نبع الماء اللتي يشرب منها التنين فنضع له سما هناك. لكن هذا السم لا يقتل التنين بل يصبه فقط هو وذريته بتشوهات خلقية. فينكمش عنق التنين الى النصف. واذا أفترضنا ان ذاك التنين هو أيضا تربيعى! بمعنى ان صار عنقه النصف فان قوة نيرانه اللتى يبثها من فمه ستنخفض الي الربع فلاشك اننا سوف نكون قدد حققنا تفوقا عليه. لكن ماذا اذا كان التشوه الخلقى يفعل أكثر من ذلك فأصبح له أربعة اعناق بدلا من عنق واحد؟ هنا لا نكون قد حققنا أى شئ فاربعة أعناق ولكل عنق ربع القدرة السابقة نكون قد عدنا الى المشكلة الاصلية. اما اذا أصبح له بعد هذا التشوه عشرة أعناق فنكون فى هذه الحالة خسرنا ولم نكسب!

مثالا أخر اكثر واقعية: دعونا نفترض اننى اريد ان ابنى منزلا ولكن ليست لى القدرةعلى شراء احجار البناء بالكامل فاقرر تقسيم المشكلة وبناء طابقا طابق واشترى الإحجار اللازمة لذلك فقط. لكن هنا يقول لى تاجر احجار البناء: لا.  السعر سيختلف فى هذه الحالة. السعر الأول كان فى حالة الشراء بالجملة اما اذا كنت تريد شراء كمية أقل فسعر الوحدة من احجار البناء سوف يرتفع. اذن لاشك ان التكلفة النهائية سترتفع فى النهاية. لكن أنا لم يكن لى من البداية القدرة على انهاء الهدف الا بهذه الصورة. فهذه التقنية لها ثمنها اللذي يجعلها فى النهاية اكثر كلفة. لكن مع ذلك لها ما يسوغها حين لا تتوفر القدرة او حتى لاراحة الرأس. فالتعامل مع مشكلة معقدة هو امر مزعج جدا. ومن الافضل تفتيتها الى مشاكل أبسط بحيث يكون حل هذه المشاكل الأبسط جميعا يؤدي الى حل المشكلة الاصلية. ربما تكون التكلفة النهائية أعلى.لكن اراحة الرأس وانجاز الأهداف هى ايضا أمور لها أعتبارها حتى وان لم يكن ماديا مباشرا.  لكن فى حالة اجراء عملية الضرب من خلال جهاز الكمبيوتر فما يهمنا فعلا هو توفير الزمن الكلى فلا يجوز ان يزيد تطبيق تقنية فرق تسد من الزمن.

وهنا دعونا مرة اخرى نتذكر القواعد اللتى رأيناها فى المرات الماضية:
1 ضرب عددين كلاهما من خانة واحدة يحتاج الى خطوة واحدة
2 جمع عددين كلامهما من خانة واحدة يحتاج الى خطوة واحدة
3 ضرب أى عدد فى الاعداد الخاصة: 10 أو 100 أو 1000 الى أخره يحتاج الى خطوة واحدة
4 لا يمكننا ان نجري اي عمليتين من العمليات السابقة فى نفس الوقت. ولأجراء عمليتين منهما نحتاج الى خطوتين متتاليتين

لكن ما هى الحيلة اللتى نقسم بها الأعداد ولا تغير النتيجة النهائية؟ الاجابة بسيطة ونعرفها من ميدان الجبر. أنها عملية ضرب الأقواس حيث نعرف كلنا التالي:
(a+b)(c+d)=ac+ad+bc+bd
فاذا شئنا مثلا ضرب 82 فى 73 فنستطيع أن نحول تلك العملية الى الصورة التالية
82*73=(8+2×10)(7+3×10)

لكن دعونا نحصل على اجابة عامة بتحويل الأرقام الى رموز مرة اخرى. فدعونا نفرض أن العدد الاول هو ba والعدد الثانى هو dc حيث ترمز a الى احاد العدد الأول او الى العدد 2 بينما ترمز b الى عشرات العدد الاول أو 8 بينما ترمز c الى احاد العدد الثانى او 3 بينما ترمز d الى عشرات العدد الثانى او 7 ثم يكون التالي:
(a+10b)(c+10d)=ac+10(ad+bc)+100bd
ونرى مما سبق اننا حولنا عملية الضرب برمتها الى 4 عمليات ضرب لعددين من خانة واحدة. وهي عمليات نستطيع ان نجريها فى خطوة واحدة كما فى الأفتراض الاول. بالاضافة الى أن الضرب فى 10 و 100 هى ايضا امور يمكننا ان نجريها  فى خطوة واحدة كما فى الأفتراض الثالث. ثم علينا ان نجري عمليتى جمع. وهى عمليتان خطيتان وفى أسوأ الحالات تحتاج عملية الجمع الواحدة الى 4 خطوات كما رأينا فى المرات الماضية. فيكون عدد الخطوات المطلوبة هو 14خطوة. وهى نتيجة لا تختلف كثيرا عن الطريقة المدرسية اللتى احتاجت الى 13 خطوة لفعل نفس الأمر كما رأينا فى المرات السابقة. لكن ما أود ان أنبه اليه هنا هو نتيجة عملية التقيسم. فقد حصلنا على 4 عمليات ضرب جديدة ابسط لكننا لم نوفر أى شئ. فلقد حصلنا على تنين  ذي اربعة رئوس أصغر. هذا كل ما حدث حتى الأن! مع ذلك دعونا نستفيض فى الحديث حول هذا الأمر.

ماذا اذا كنا نريد ضرب عددين من 4 خانات فى بعضهما مثلا 5482 في 9673 . مرة اخرى علينا ان نقسم الاعداد الى الصورة التالية:
5482×9673=(54+82×100)(96+73×100)
ومرة اخرى نحصل على 4 عمليات ضرب جديدة لكن هذه المرة لعددين من خانتين. مثلا علينا أن نضرب 82 فى 73 .ونحن هنا مرة أخرى لن نجرى عملية الضرب مباشرة لكننا سنحيلها كما رأينا فى المثال العددي السابق الى 4 عمليات لضرب عددين من خانة واحدة. ويكون علينا فى النهاية أجراء 16 عملية ضرب لأعداد من خانة واحدة بخلاف عمليات الضرب الخاصة فى 10 و 100 و 10000 ثم عمليات الجمع ذات التعقيد الخطي. ولهذا نرى انه التعقيد ما زال تربيعى.

اذن فقد حصلنا على خوارزمية ثالثة جديدة لاجراء عملية الضرب لكنها لم توفر لنا  شيئا حتى الأن فمازال التعقيد تربيعى. لكن مع ذلك دعونا نمضى مع هذه الخوارزمية لنرى كيف يصنعها المبرمجون. ففهم ذلك الأمر مهم بالنسبة لنا اليوم.

أنهم لأجل ذلك يكتبون برمجيات ذاتية الاستدعاء recursive تقوم باستدعاء نفسها مرارا وتكرارا لكن فى كل مرة بقيم ابسط حتى تتمكن من اتمام مهمتها. وهذه التقنية تصيب الكثيرين من المبرمجين المحترفين بصداع الرأس عندما يتتبعون طريقة حدوثها. مع ذلك سنحاول هنا ان نقدمها بصورة  بسيطة وواضحة. الامر اشبه بهيكل شجري. حيث نبدأ من جزع واحد ينقسم الى افرع كبيرة ومن الأفرع الكبيرة تنبثق أفرع صغيرة ومن الأفرع الصغيرة تخرج أفرع أصغر حتى نصل الى الأوراق اللتى لا يأتى شئ بعدها. فالتقنية اللتى يتبناها المبرمجون هنا اشبه بنسيج يبدأون بغزله من الجزع باتجاه الأفرع والأوراق وبعدما يبنونه ببدأون بنقضه من أسفل الى أعلى من الأوراق وتصاعديا حتى يصلوا الى نقطة البداية مرة اخرى لكن ذلك بعد ان يكونوا قد ضموا كل رحيق الاوراق لديهم.

دعونا نمثل ذلك بدولة تريد ان تحصل من مواطنيها على شئ ما. ربما يكون ذلك الشئ اصواتهم الأنتخابية او تبرعات مالية او ضرائب أو أى شئ ما أخر. دعونا نفترض ان تلك الدولة تتكون من 4 محافظات أو مديريات او ولايات او قضاءات كيفما تكون الكلمة فى الدول العربية المختلفة. وكل واحدة من هؤلاء تتكون بدورها من 4 مدن. وكل مدينة تتكون من 4 احياء. وكل حي يحتوى على 4 مقرات لاستقبال المواطنين. وكل مقر يستقبل 4 أسر. وكل أسرة تتكون فى النهاية من زوج وزوجة يمثلان عملية ضرب عددين من خانة واحدة. وبعد ان تتمكن الدولة من أقامة هذا التقسيم الأدارى او  حتى بفرض انه كان موجودا بالفعل تبدأ عملية جمع الاصوات او التبرعات فى تاريخ معين ولنقل ان العملية تبدأ فى التاسعة صباحا. دعونا نرى مقاربة اولى لكيفما تتم تلك العملية.

فى التاسعة صباحا  تذهب الاسر رقم 1 الى المقرات  القريبة منها وبفرض ان تلك  العملية مخصص لها ربع ساعة. اذن في الساعة التاسعة والربع ستبدأ الأسر رقم 2 بالذهاب الى المقرات الخاصة بها. وفى  تمام الساعة العاشرة ستكون كل الاسر فى كل ارجاء الدولة قد اعطت ما ينبغى منها. ثم تبدأ المقرات فى تقدير قيمة ما حصلت عليه. فدعونا نفرض دائما ان الأسر رقم واحد فقيرة بينما الثانية والثالثة متوسطة الحال والرابعة ثرية ومقرات المواطنين تعلم ذلك وتفرض ان ارقام الاسرة رقم واحد هى ارقام تدخل كما هى. بينما الاسر الثانية والثالثة الأرقام اللتى يعطونها يجب ضربها فى 10 لأن هذا ما يعنونه. بينما الأسرة الرابعة يجب ضرب قيمة مايقولونه فى 100 ثم تجمع تلك النتائج معا للحصول على قيمة ما تم تحصيله فعلا. لاحظوا ان هذه العملية تشبه الحساب فى المثال العددي السابق. ولنفرض ان تلك العملية تستغرق نصف ساعة. اذن فى العاشرة والنصف ستكون كل المقرات قد انتهت من عملها. الأن تبدأ المقرات فى تصعيد نتائجها الى الأحياء الخاصة بها. حيث تبدأ المقرات رقم 1 فى رفع نتائجها فى الساعة العاشرة والنصف ولمدة نصف ساعة مثلا. ثم تليها المقرات رقم 2 ثم 3 و 4. اذن فى الساعة الثانية عشر والنصف تكون المقرات قد انتهت من رفع ارقامها. فتبدأ الأحياء فى عمل حساباتها. حيث مرة اخرى تفترض ان المقرات الاولى دائما فقيرة والثانية والثالثة متوسطة الحال والرابعة افضل حالا. لذلك تضرب الاحياء قيم المقرات الثانية والثالثة فى 100 بينما قيم المقرات الرابعة فى 10000 . ثم تبدأ الأحياء فى رفع قيمها للمدن بصورة مشابهة. وتقوم المدن بعمل حساباتها بصورة مشابهة وترفع ارقامها للمحافظات. ثم ترفع المحافظات قيمها للدولة المركزية

وهذا المثال السابق يشبه عملية ضرب عددين من 32 خانة فى بعضهما. حيث يمكن تقسيمهما على 5 مراحل الى اعداد من 16 خانة ثم 8 ثم 4 ثم 2 ثم 1 تماما كما يمكن تقسيم الدولة الى محافظة ومدينة وحي ومقر وأسرة. لكن هذا الامر ليس قاصرا على 32 خانة فقط . بل يمكننا فعل ذلك لمالانهاية من المرات. فيمكننا تخيل مثلا ان كل 4 دول يشكلون قارة وكل 4 قارات تشكل كوكبا وكل 4 كواكب تشكل مجموعة شمسية وكل 4 شموس تشكل مجموعة نجمية وكل 4 مجموعات نجمية تشكل مجرة وكل 4 مجرات تشكل كونا وكل 4 أكوان تشكل كونا أكبر وهكذا حتى مالانهاية!

لكن الكمبيوتر لا يعمل وفق تلك المقاربة الأول. فكما قلنا فى الشرط الرابع ان الكمبيوتر لايمكنه ان يجرى عمليتين فى نفس الوقت فالكمبيوتر لديه معالج بيانات او بروسيسور واحد Processor يقوم بالخطوات الواحدة تلك الاخرى. وبالتالى على عكس المقاربة الاولى لايمكن للمقرات الانتخابية المختلفة ان تفتح ابوابها فى نفس الوقت كما يحدث فى الواقع.  ويمكننا تمثيل ذلك بان تلك الدولة العجيبة لديها راية واحدة من يحملها هو من يقوم فعلا بالخطوة الحالية وهو من يحظى فعلا باهتمام البروسيسور. اذن دعونا نرى المقاربة الثانية اللتى توضح كيف يعمل الكمبيوتر.

أن من يحمل الراية فى البداية طبعا هى الدولة المركزية اللتى تبدأ فى التاسعة صباحا باعطاء الامر لبدء عملية الجمع. لكن الدولة لا تستطيع ان تقوم بعملية الجمع بنفسها وهى تعلم طبعا انها تتكون من 4 محافظات. فتطلب من المحافظة الاولى ان تجمع ارقامها. وعلى الدولة المركزية ان تنتظر طوال الوقت حتى تعود المحافظة الأولى بالأجابة وتسلمها الراية مرة أخرى. حيث تستطيع الدولة بعد ذلك أن تطلب نفس الأمر من المحافظة الثانية ثم الثالثة ثم الرابعة. اذن على المحافظة الاولى ان تجمع من رعاياها. لكنها أيضا لا تقوم بذلك بنفسها فتسلم الراية للمدينة الاولى وتطلب منها ان تجمع بياناتها وبعد ان تعود المدينة الاولى ببياناتها تطلب نفس الأمر من المدينة الثانية ثم الثالثة ثم الرابعة. ثم تقوم المحافظة بحساباتها وتعود للدولة بالنتيجة. اذن المدينة الاولى فى المحافظة الاولى حصلت على الراية لتعطيها للحى الاول ليعطيها للمقر الأول ليعطيها للاسرة الاولي ثم الاسرة الثانية فالثالثة والرابعة . وبهذا ينتهى المقر الاول فيعمل حساباته ويعيد الراية الى الحى الاول اللذى يطلب نفس الشىء من المقر الثانى ثم الثالث ثم الرابع وتعود الراية اخيرا الى المدينة الاولى فتكرر نفس الطلب من الحى الثانى. الى اخره. وطوال هذا الوقت تنتظر المحافظة الاولى ناهيك عن الدولة المركزية. لكن هكذا فعلا يعمل جهاز الكمبيوتر. فقط خطوة واحدة فى نفس اللحظة.

اذن حان الوقت اخيرا للحيلة الرياضية اللتى تكلمنا عنها سابقا . واللتى تجعل للتنين ثلاثة رؤوس فقط بدلا من اربعة. وبها نحصل على خوارزمية جديدة ذات كفاء أعلى.

كان استاذ الرياضيات الروسى اندريه كولمجروف يعتقد انه لا توجد طريقة لعملية الضرب تعقيدها افضل من التربيعي. وكان يعتقد ان الطريقة المدرسية وان لم تكن أفضل طريقة فانها ليست بعيدة عن أن تكون ذلك. وقام بتنظيم مؤتمر فى عام 1960  بداخل جامعة موسكو لاجل ذلك الشأن. وقام بجمع الابحاث العلمية وتنظيم المحاضرات لهذا الغرض. وفى أجواء هذه المناسبة توصل طالب ابن ثلاثة وعشرين ربيعا فى ذلك الوقت وفى ظرف أسبوع واحدى الى حل أستطاع ان يفتت فيه عملية ضرب القوسين الى 3 عمليات ضرب وليس 4 كما رأينا حتى الأن. وكان هذا الطالب هو الشيشانى اناطولي كاراتسوبا Karatsuba . واخبر كاراتسوبا كولمجروف بطريقته اللتى انبهر بها وعرضها على المؤتمر العلمى وقام بنشرها كرسالة علمية حتى بدون علم كاراتسوبا اللذى تفأجأ بالرسالة العلمية بعد ان طبعت وان كانت تحمل أسمه.

لكن ماهى تحديدا تلك الحيلة الرياضية اللتى اكتشفها كاراتسوبا؟ تعالوا نراها مطبقة على المثال السابق الخاص بضرب عددين من خانتين. فخطوات الطريقة هى كالتالي:
1 نحسب القيمة ac اى نضرب 2 فى  3 ونحتاج لذلك خطوة واحدة والنتيجة هى 6
2 نحصب القيمة bd أي نضرب 7 فى 8 ولذلك نحتاج خطوة واحدة والنتيجة هى 56
3 نصل الأن الى نقطة غريبة علينا ان نحسب الفرق a-b وهذا الامر قد يرتبط بصعوبة تقنية ولكننا سوف ننتجاوزها اليوم فالنتيجة قد تكون عددا سالبا. ونحن لم نتحدث حتى الأن حول الأعداد السالبة. لكن لابأس سنفرض ان عملية الطرح تتم تماما كعملية الجمع. اذن الناتح من هذه الخطوة هو طرح 8 من 2 النتيجة هى اذن سالب ستة وعدد الخطوات المطلوبة هو خطوة واحدة
4 الخطوة الرابعة كالخطوة السابقة تماما فعلينا ان نفعل ذلك الشئ الغريب ونطرح c-d والنتيجة هي سالب أربعة وعدد الخطوات هي خطوة واحدة
5 نضرب العددين من الخطوتين السابقتين فتكون النتيجة هى 24 وهذه هى عملية الضرب الثالثة والأخيرة وتحتاج الى خطوة واحدة.
6 والأن نصل الى قلب الحيلة فعلينا ان نطرح نتيجة الخطوة السابقة من مجموع  الخطوتين الاولى والثانية لنحصل على باقى نتائج ضرب القوسين وذلك للأتي
ac+bd-(a-b)(c-d)=ac+bd-ac-bd+ad+bc=ad+bc
او نحسب تحديدا التالي 56+6-24 والنتيجة هى 38 وعدد الخطوات المطلوبة لجمع 56 على 6 هي خطوتين ولطرح 62 من 38 ايضا خطوتين
7 نضرب النتيجة السابقة فى 10 ونحتاج لذلك خطوة واحدة والنتيجة هى 380 ونضرب العدد الناتج من الخطوة 2 فى 100 ونحتاج لذلك أيضا خطوة واحدة والنتيجة هى 5600
8 الخطوة الأخيرة نجمع النتيحة من الخطوة الاولى على نتائج الخطوة السابعة: او نجمع 6 زائد 380 زائد 5600 لنحصل على النتيجة النهائية 5986 وهى النتيجة السليمة. وعدد الخطوات من عمليتين الجمع هاتين هما 3 خطوات لجمع 6 زائد 380 ثم 4 خطوات لجمع 386 على 5600
9 اذن النتيجة النهائية هى 5986 وعدد الخطوات الكلية هى 18 خطوة. لاحظ ان الطريقة المدرسية تحتاج بحد أقصى الى 13 خطوة للوصول للنتيجة النهائية

لقد احتجنا اذن الى خطوات أكثر!. لكن لاداعى للقلق. فطريقة كاراتسوبا تعطى أكلها عندما يزداد عدد خانات الأعداد اللتى نجري بشأنها عملية الضرب. لكن لابد هنا ان يلوح لنا تساؤلان . الاول هل هناك برهان رياضي على ذلك؟  والتساؤل الثانى كيف نستطيع ان نفسر ذلك فى ضوء عمليات الأستدعاء الذاتى المعقدة اللتى رأيناها سابقا؟. دعونا نبدأ بالتساؤل الثانى أولا.

الأمر يشبه اربعة اشخاص يذهبون الى مطعم ويجلسون الى طاولة واحدة وفى النهاية يطلبون النادل من أجل الحساب اللذي يحاسبهم فردا فردا. فلو فرضنا ان كل شخص يحتاج الى 5 دقائق فانهم جميعهم سيحتاجون الى 20 دقيقة والنادل سيكون متضايقا جدا أذا أخذ شخص اكثر من 5 دقائق لأن هذا يؤثر على باقى عمله مع الزبائن الأخري! لكن فى الحياة العامة أحيانا يجرى الأمر غير ذلك. فقد يقوم هؤلاء الأشخاص بالحساب فيما بينهم ثم يتولى شخص منهم الحساب عنهم جميعا. هذا يكون اسرع للنادل لانه يحتاج ان يتعامل مع شخص واحد فقط. اما فى حالة خوارزمية كاراتسوبا فالأمر لا يجري على ذلك المنوال تماما. فهؤلاء الاربعة اشخاص يقومون بالحساب فيما بينهم. ولكنهم يحاسبون النادل كما لوكانوا ثلاثة فقط. ويقولون له سـتأخذ الحساب كاملا لكن عاملنا كأننا ثلاثة موجودين فقط. وأعط لكل واحد 6 دقائق بدلا عن 5. فلا شك ان النادل سيكون سعيدا بهذه النتيجة لانه سياخذ حسابه كاملا ويتم توفير وقته. بل وربما يكون النادل هو ذلك الشخص الذكي اللذى يلاحظ ان الشخص الثانى والثالث طلباتهم متشابهة مثلا فيحصل المال من الشخصين الأول والرابع فقط ثم يقوم بتحريك الأطباق بطريقة معينة من هنا الى هناك لأن هذا يجعله يحسب القيمة المطلوبة بشكل أسرع.

ويمكن تعميم العملية السابقة. فنفترض ان قاعة المطعم تتكون من 4 طاولات ومن أجل توريد الحساب النهائى يتم التعامل معهم كأنهم ثلاثة فقط. كما أن المطعم يتكون من 4 قاعات سيتم التعامل معها كأنها ثلاثة وهكذا! وفى حقيقة الامر فلن يوفر النادل شئ من الوقت بل العكس لكن المستويات الأعلى هى من تستفيد بذلك. دعونا نوضح ذلك بمثال الدولة السابق.

فايضا مقرات المواطنين تعلم ان لديها 4 أسر لكنها تستدعى 3 فقط لتحصل على النتيجة الاجمالية السليمة وكذلك الاحياء ستستدعى 3 مقرات والدولة ستستدعى 3 محافظات. ومن السهل ان نرى كيف يتم توفير الوقت. فكما رأينا فى المثال السابق ان الدولة كان عليها ان تنتظر ردها طويلا من الزمن حتى تعود اليها المحافظة الرابعة بنتيجتها الاجمالية. الأن ستوفر الدولة نداء المحافظة الرابعة بكل ما تحمله تحتها من تفرعات شجرية رباعية. صحيح ان هناك العديد من الحسابات الأضافية سوف تتم لكن الوقت اللازم سوف يتم تعويضه وذلك لسببين

الاول ان تلك الحسابات الأضافية تتم على مستوى اعلى نسبيا فهى تتم على مستوي المقرات بالنسبة للأسر وعلى مستوي المحافظات بالنسبة للمدن الى أخره. كما أن تعقيد هذه الحسابات خطي
الأمر الثانى وهو الأهم ان هذا الأمر برمته يشبه عملية الأنشطارات النووية. وهذا ماينتج عنه فى النهاية كثرة أوراق الهيكل الشجري. وفى الحالة الاولى كانت عندنا انشطارات رباعية. لكن فى الحالة الثانية سيختفى الفرع الرابع بأكمله بكل ما ينضوى تحته من تفرعات رباعية. كما أن الافرع الثلاثة المتبقية لن تنبثق عنها أفرع رباعية جديدة بل ثلاثية فقط. لذلك يمكننا بسهولة ان نرى انه مع تعدد مستويات الأنشطار سيربو النقص الحادث فى عدد الأفرع الناشئة على عدد الحسابات ألاضافية الجديدة.

والأن ما هو تعقيد هذه الطريقة؟ لحساب ضرب عددين لهما n من الخانات نعمل دائما الخطوات التالية:
1 نحسب 3 مرات عملية الضرب لعددين لهما نصف عدد الخانات
2 قبل أن نحسب عملية الضرب الثالثة علينا أن نعد مدخلاتها. وذلك عن طريق عمليتى طرح لعددين لهما n/2 من الخانات. اذن عدد الخطوات المطلوبة لهذه العملية هو n من الخانات
3 بعد اجراء عمليات الضرب. نجمع اثنين منهما ولهما n من الخانات . اذن عدد الخطوات المطلوبة هو أيضا n والناتج قد يكون له n+1 من الخانات. ثم نطرح النتيجة من ناتج عملية الضرب الثالثة اذن عدد الخطوات هو n+1 ثم نضع عددا من الأصفار على يمين عددين وهذا يتطلب خطوتين. ثم نجري عمليتي جمع لكل منهما 2n من الخطوات

اذن التعقيد الكلى هو
O(n)=3.O(n/2)+7n+3
بينما تعقيد الطريقة المدرسية كان
O(n)=4n^2-n-1

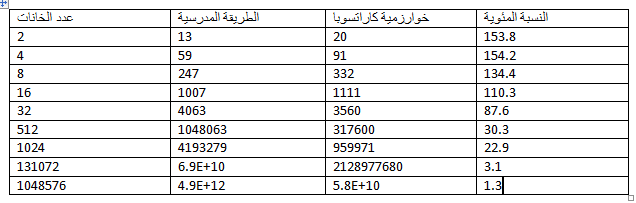
ونقارن بين نتائج الطريقتين فى الجدول التالي

ونلاحظ ان خوارزمية كاراتسوبا تؤتى ثمارها عندما يصبح عدد الخانات 32 خانة . وهذا ليس أمرا نادرا حيث سبق وقلنا ان الكمبيوتر يعبر عن الأعداد في صورة النظام الثنائى وهو نظام مريض بالتضخم كما وضحنا المرة الماضية. كما أن جهاز الكمبيوتر لا يتعامل مثلنا مع الأعداد بالخانات. لكن اقل طول يتعامل معه الجهاز هو مضاعفات البايت Byte . والبايت له 8 خانات. ونرى من الجدول أننا عندما نضرب عددين من 1000 خانة تصبح طريقة كارتسوبا أقصر ب 75% واذا كانت عدد الخانات مليون خانة لصارت تللك الطريقة أقصر بحوالى 99%

الأن نعلم ان هذه الطريقة تعقيدها الزمني ليست تربيعيا لكن الى أي عائلة تنتمى هذه الخوارزمية؟ كما سبق ورأينا فان عدد الخطوات يعتمد على عدد الانشطارات الثلاثية اللتى تحدث جراء تلك الطريقة. ورأينا اننا عند ضرب عددين من  خانتين احتجنا لثلاث عمليات ضرب. ولضرب عددين من 4 خانات احتجنا الى 9 عمليات ضرب . ولضرب عددين من 8 خانات سنحتاج الى 27 عملية ضرب اذن عدد عمليات الضرب هو 3 مرفوعة للوغاريتم n وهى نتيجة يمكن تحويلها الى n اس لوغاريتم 3 أو n^1.5849 . وهذا هو ما يصنع الفارق.