تخفي عن الناس سنا طلعتك
وكل ما في الكون من صنعتك
فأنت مجلاه وأنت الذي
ترى بديع الصنع في ايتك
ماهي العلاقة بين الهندسات الغير اقليدية وهذه الأبيات شعرية اللتى غنتها أم كلثوم من الحان رياض السنباطي و كلمات أحمد رامي؟ العلاقة هو نابغة مهضوم الحق فى الشرق و الغرب اسمه عمر الخيام. وذلك الأسم نعرفه جميعا لأننا قد نكون مهتمين بالأدب أو من المعجبين بأغنية ام كلثوم المعروفة برباعيات الخيام أو فى أضعف الاحوال قرأنا هذا الأسم مطبوعا او مضيئا على ابواب أحد المطاعم أو الفنادق فى أحد البلاد العربية! لكن هناك أيضا أسباب أخرى. فمن هو عمر الخيام؟
عمر الخيام كان رياضيا وفلكيا وفيلسوفا وشاعرا بالاضافة الى اشياء اخرى ولد فى مدينة نيسابور الأيرانية عام 1048 ميلادية وكانت وفاته فيها ايضا عام 1131. أى انه عاش قبل 1000 عام تقريبا. وكان الخيام عبقريا موسوعيا درس الفلسفة ودرسها وكان متأثرا جدا بابن سينا وكان يسميه -كما كل تلامذته- الشيخ الرئيس. وكان الخيام ايضا فلكيا لامعا ساهم فى تطوير التقويم الفارسي. اما انجازاته الرياضية فهى عديدة منها انه أول من حل معادلات الدرجة الثالثة بطريقة هندسية تحيليلة. كما انه توصل لحل معادلات الدرجات الأعلي واستخدم فى ذلك ما يعرف اليوم باسم مثلث باسكال.
وكان فى بلاد فارس فن شعري يعرف بالرباعيات وهي اربعة ابيات تشترك كلها فى نفس القافية أو قد يختلف البيت الثالث احيانا. ونظم الخيام بعضا من هذه الرباعيات وارتبط اسمه بها. فطمست شهرة الخيام الشاعر شهرة الرياضى والفلكي والفيلسوف. ذلك على الرغم من انه لم يكتب الرباعيات كلها بل وهناك البعض اللذى يشكك في ان الخيام العالم ليس هو الخيام الشاعر أساسا. لكن الراجع انه نظم بعض هذه الرباعيات اللتى نالت شهرة عالمية واسعة وترجمت الى كثير من اللغات . وقد كانت جميع كتابات الخيام العلمية والفلسفية باللغة العربية. فقط الرباعيات كانت بالفارسية وقد ترجمها الى العريبة عديدون ابرزهم الشاعر احمد رامى. وبعض هذه الرباعيات غنتها ام كلثوم.
و ما يهمنا اليوم هو كتاب للخيام اسمه “رسالة فى شرح ما أشكل من مصادرات كتاب اقليدس” تناول فيه المسلمة الخامسة ووضع فيه أول نظريات الهندسات الغير اقليدية حتى وان كان هو نفسه لم يدرك ذلك. لكن دعونا نستعرض الموضوع من بدايته.
كانت المسلمة الخامسة تشكل فى الماضى غصة فى حلق الرياضيين وكانت مصدر قلق بالنسبة لهم فقبلوها حتى اشعار اخر. فصياغة المسلمة الطويلة تجعلها اقرب الى أن تكون نظرية او نتيجة منها الى ان تكون مسلمة اولية. ولذلك حاول الكثيرون الاستغناء عن هذه المسلمة وبرهنتها بدلالة المسلمات والبديهيات الأخرى. ونكفي مثالا لهؤلاء ان نذكر الرياضى والفيزيائي العظيم الحسن ابن الهيثم اللذى كان يسمى فى الغرب ببطليموس الثانى. لكن كان برهان ابن الهيثم خاطئا وكذلك كانت براهين غيره. فهم جميعا استخدموا بدون أن يدركوا افتراضات رياضية ليست مستقلة عن المسلمة الخامسة: كمسلمة التوازى لبلايفير Playfair او انطلقوا من قاعدة ان مجموع زوايا المثلث الداخيلة تساوى قائمتين او أن البعد بين الخطين المتوازيين يبقى دائما ثابت.وهذه كلها افتراضات تكافئ المسلمة الخامسة لاقليدس. فكانوا كمن يفسر الماء بالماء.
اما الخيام فقد رفض برهان ابن الهيثم و اخذ منحى مغايرا. فلم يحاول ان يبرهن المسلمة الخامسة بدلالة المسلمات الأربعة الاول كما فعل غيره بل استبدلها بمسلمة اخرى مكافئة لأرسطو تقول: “اي مستقيمين متقاربين لابد ان يلتقيا ومن المستحيل ان يتباعدا مرة اخرى فى اتجاه تقاربهما”. ومن هذه المسلمة استطاع اثبات مسلمة اقليدس الخامسة. وليس فى هذا أى جديد كما رأينا حيث ان الصياغتين متكافئتان. لكن الجديد ان عمر الخيام استطاع ان يكتشف اول نظريات الهندسة الغير اقليدية بمساعدة شكل رباعى الأضلاع يعرف برباعى ساتشيري. ودعونا نوضح ذلك بالمثال التالي:
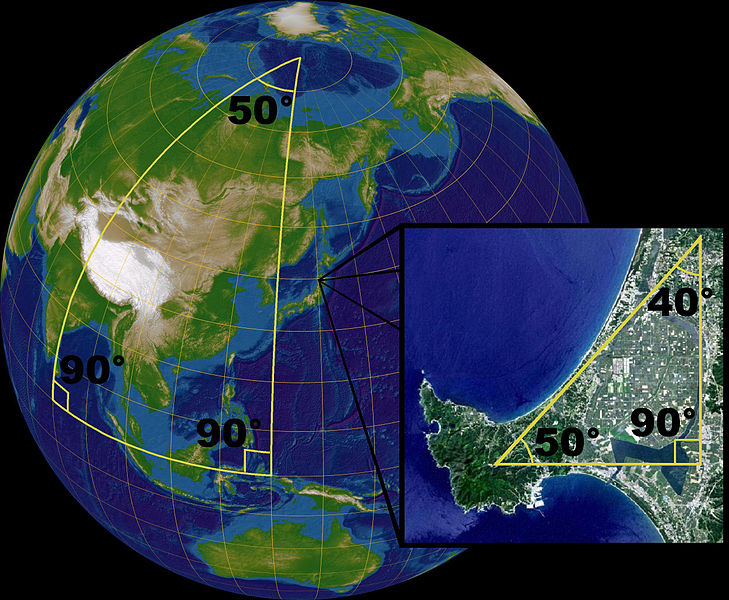
لو افترضنا اننا من نقطة ما انطلقنا 1 كم باتجاه الجنوب ثم أتبعناها ب 1 كم باتجاه الشرق ثم اخيرا 1 كم باتجاه الشمال. فماذا سوف يكون بعدنا عن نقطة البداية؟ هل سيكون1 كم باتجاه الشرق؟ لا تكن متأكدا من ذلك! فذلك يتوقف علي هندسة المكان اللذي نحن موجودون فيه! مثلا لو تخيلنا اننا نقف عند نقطة القطب الشمالى ثم سرنا 1 كم على امتداد خط جرينتش أو خط الطول رقم صفر مسافة 1 كم باتجاه الجنوب. ثم سرنا 1 كم على خط العرض الموجود هناك باتجاه الشرق. فاذا سرنا مرة اخرى 1 كم باتجاه الشمال فسنصل الى القطب الشمالى مرة اخرى. وسيكون بعدنا عن نقطة البداية هو صفر!! اما اذا انطلقنا من نقطة تقع على خط الاستواء او كان سطح الارض ليس كرويا بل مستويا كورقة فى كتاب فاننا اذا كررنا نفس الخطوات السابقة فسيكون بعدنا عن نقطة البداية هو 1 كم باتجاه الشرق تقريبا!!
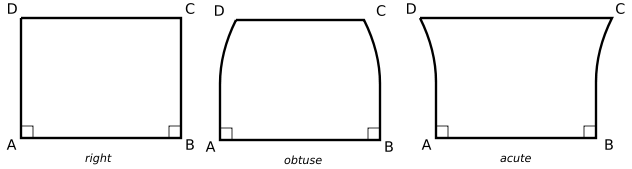
ومضلع ساتشيري هو شكل رباعى الاضلاع يتكون من قاعدة وعموديين فوقها متساويين الطول ثم يكمل الضلع العلوى الشكل الرباعى. وهنا يظهر سؤال هل الزاويتان بالأعلى قائمتان بالضرورة ام قد تكونا حادتين او منفرجتين؟ أوضح الخيام ان الزاويتين بالاعلى دائما متساويتان. وهما قائمتان فى حالة سريان المسلمة الخامسة لاقليدس. لكن من الممكن ان تكون الزاويتان ايضا حادتين او منفرجتين بدون اى تناقض طالما لا تحتوى لائحة مسلماتنا الاولية على أي من المسلمة الخامسة أو احدى مثيلاتها!
ثم تمضى 7 قرون تقريبا حتى القرن الثامن عشر ونصل الى جيوفانى ساتشيري Giovanni Saccheri وهو رياضى ايطالى ينتمى الى رهبانية اليسوعيين المشهورة بدعمها للعلوم والرياضيات.وكتب ساتشيرى كتابا حول هذا الموضوع. لكن يقلقنا سؤال هل كان ساتشيري يعرف عمر الخيام وأعماله ام لا؟ فقد اعاد ساتشيري انتاج عمر الخيام بدون ان يذكر اسمه. فاذا كان ساتشيرى يعرف الخيام فقد ارتكب سرقة علمية كبيرة. وحتى الشكل اللذى يعرف بمضلع ساتشيرى الرباعي من العدل و الأصوب ان يسمى مضلع الخيام الرباعي. وهم فقط فى ايران يسمونه كذلك . لكن ما هو ثابت أن ساتشيري كان يعرف نصر الدين الطوسى تلميذ الخيام فقد انتقده فى كتابه. والطوسى هو من نسخ النسخة اللتى وصلت الينا من كتاب الخيام.
لكن دعونا ننحي هذا الجدل جانبا ونرى ماذا فعل ساتشيري. أراد ساتشيري ان يبرهن المسلمة الخامسة لأقليدس وذلك عن طريق مايسمى بالبرهان المعكوس او البرهان بالتناقض وهو نوع من الاثباتات يفرض فيه الأنسان فى البداية عكس مايريد ان يصل اليه حتى يصل الى نتائج متناقضة فيترتب على ذلك ان العكس خاطئ و الصواب هو الأصل. واستخدم ساتشيري أن مجموع زوايا المثلث الداخلية يساوى 180 درجة -وهى كما نعلم مكافئة لمسلمة اقليدس الخامسة. فأفترض ساتشيرى اولا ان مجموع زوايا المثلث اكبر من 180 درجة ووصل الى ان هذا ممكن فقط عندما يكون الكون أو المكان باسره منتهى و وهذا يتعارض مع مسلمة اقليدس الثالثة ولذلك رفض هذا الطرح. ونعلم اليوم أن الهندسة الأهليليجية elleptic geometry وهى احد انواع الهندسات الغير اقليدية لا تخالف المسلمة الخامسة فقط بل الثالثة ايضا وفيها مجموع زوايا المثلث فيها اكبر من قائمتين. ثم بحث ساتشيرى معقولية ان يكون مجموع زوايا المثلث اقل من 180 درجة ولكنه لم يستطع ان يصل الى اى تناقض. فوصل الى نتائج تبدو مجنونة بالنسبة للكون اللذي نعيس فيه وللهندسة اللتى نعلمها ولكنها ليست متعارضة فيما بينها. هذا دفع ساتشيرى الى ما يشبه الأستسلام ويقدم فى النهاية استنتاجا ركيكا مقارنة بالمجهود المبذول سابقا فيقول: فرضية أن تكون مجموع زوايا المثلث الداخلية اقل من 180 درجة أمر مرفوض لان ذلك يتنافى مع طبيعة الخط المستقيم.
ثم نصل فى نهاية القرن الثامن عشر الى الرياضي السويسري يوهان لامبرت Lambert اللذي سار على نفس الخط اللذى سار عليه ساتشيري ولكنه لم يرتكب نفس الخطأ فيرفض أن يكون مجموع زوايا المثلث اقل من 180 درجة للسبب السابق. بل استطرد فى الاستنتاجات و أكتشف قوانين اكثر غرابة. اكتشف لامبرت ان الفرق بين مجموع زوايا المثلث والقائمتين يتناسب دائما مع مساحة المثلث! كما اكتشف ايضا ان المثلث مهما كبر فهناك حد اقصى تصل اليه مساحته ولا يمكن ان يتخطاه!! ثم اكتشف لامبرت امرا اكثر غرابة واثارة وهو ان خواص هذا المثلث تكافئ خواص مثلث مرسوم على سطح كرة ذات نصف قطر يساوى عددا تخيليا! و الأعداد التخيلية كما نعلم هى الاعداد اللتى اذا ضربناها فى نفسها تعطى رقما سالبا!
مع هذا فان اكتشاف الهندسة الغير اقليدية لا ينسب الى لامبرت ولكن الى اخرين. ويعلق الرياضى الانجليزي بنروز على هذا الامر فيقول: انه نوع من الاجحاف فى حق لامبرت الا يتم اعتباره من مكتشفى الهندسة الغير التقليدية ولو بشكل جزئي.
ثم حدثت فى القرن التاسع عشر مفاجأة قلما تتكرر فى الزمان. فقد ظهر فجاءة ثلاثة رياضيين من ثلاثة دول مختلفة وقام كل منهم باكتشاف الهندسة القطعية الزائدية Hyperbolic geometry وهى احد انواع الهندسة الغير اقليدية بشكل مستقل وفى نفس الوقت تقريبا. وهؤلاء الثلاثة كانوا مجري و المانى وروسى. اما المجرى فكان يانوش بولياي János Bolyai وهو كان ابنا لاستاذ رياضيات مشهور. وتوجد مراسلات متبادلة بين الأب و ابنه كان يحاول فيها الأب صرف ابنه عن هذا الموضوع ويحذره منه ويقول له ان البحث فى موضوع المسلمة الخامسة سيصيبه بالتعاسة ويجعله يفقد كل اصدقاء بل وسيفقد معنى الحياة نفسها ويخبره انه حاول فى هذا الموضوع عندما كان شابا ولكنه لم يجن من وراءه اي خير. ولكن الابن كان مصمما على استكمال طريقه. ثم انقشعت الغشاوة امام بولياى الأبن واكتشف الهندسة القطعية الزائدية اى تلك الهندسة اللتى تكون فيها مجموع زوايا المثلث الداخلية اقل من 180 درجة.
وكان الأب صديقا للرياضى الألمانى العملاق جاوس Gauß وهنا نصل الى النجم الثانى لهذه القصة ويخبره بما حدث مع ابنه وماتوصل اليه ويسأله عن رأيه. فيجيبه جاوس بان أبنه محق وانه نفسه قد توصل الى نفس النتائج من فترة ولكنه لم ينشرها. فقد كان جاوس يخشى عاقبة ذلك. فالهندسة الاقليدية كانت اصبحت شبه مقدسة لا يجوز المساس بها وكان كبار الفلاسفة ككانت يرون فى الهندسة الاقليدية عنوانا للكمال. فخاف جاوس من ان يسبح ضد التيار السائد فصمت و اثر السلامة وكتم ما توصل اليه لنفسه. واخبر بولياى الاب ابنه برد جاوس فحزن الابن لانه كان يريد ان يكون اول من توصل الى هذا الاكتشاف. ولم ينشر جاوس نتائجه لكن بولياى الأبن نشر ماتوصل اليه فى ملحق موجود فى احد كتب ابيه.
لكن مع ذلك فان السبق فى النشر لا يعود الى بولياى ولكن الى استاذ رياضيات روسى وهو لوباتشيفسكي Lobatschewski وحيث انه اول من نشر فى هذا الموضوع فتمت نسبة الموضوع اليه ولذلك تعرف الهندسة القطعية الزائدية ايضا باسم هندسة لوباتشيفسكى. لكن بالرغم من ان كلا من بولياي و لوباتشيفسكى قد قاما بنشر اعمالها الا ان احدا لم يأبه لهما. فقط عندما مات جاوس وتم نشر اعماله فى هذا الموضوع بعد وفاته تنبه الرياضيون لهذا الموضوع. فنزول حوت كبير كجاوس البحر وسباحته عكس التيار ليس كنزول سمكتين صغيرتين فيه!
ثم اكتشف برنارد ريمان العبقرى الألمانى وأنجب تلاميذ جاوس أن هندسة الاسطح الكروية اللتى كانت معروفة منذ امد بعيد واللتى كانت تستخدم فى المساحة والهندسة الفلكية و كانت تعد جزءا من الهندسة الاقليدية اكتشف ريمان اننا اذا اعدنا النظر اليها من وجهة نظر مختلفة سنجد انها هندسة مستقلة تماما عن الهندسة الاقليدية. وبذلك كان ريمان هو مكتشف الهندسة الاهليليجية اللتى اشرنا اليها سابقا و اللتى تعرف احيانا بهندسة ريمان لانه هو مكتشفها. وفى هذا النوع من الهندسات الغير اقليدية تكون مجموع زوايا المثلث الداخلية اكبر من 180 درجة.
لكن المشكلة اللتى كانت تواجه الهندسة الغير اقليدية وخاصة هندسة لوباتشيفسكى انها ليست بديهية ولذلك يصعب تصورها و التعامل معها كما فى الهندسة الاقليدية وهنا استطاع الرياضى الأيطالى بلترامي Beltrami واللذى عاش فى الفترة بين عام 1835 حتى 1900 ان يقدم نماذج رائعة تجسد الهندسة الغير اقليدية يعيون الهندسة الاقليدية. وكانت لنماذج بلترامى الفضل في انها ازالت الشك تماما من عند الرياضيين. وأوضحت ان الهندسات الغير اقليدية هي موضوع كامل ومستقل تماما.
وتم الاعتراف بالهندسات الاقليدية بين الرياضيين ولكنها لم تكتسب شهرتها وسط غيرهم حتى ظهر البرت اينشتاين ووضع النظرية النسبية الخاصة. وقام استاذ الرياضيات مينكوفسكى بوضع رياضيات خاصة بهذه النظرية تعتمد على هنديسة لوباتشيفسكى. ثم عندما اراد اينشتاين ان يضع نظريته النسبية العامة فلم يستطع ذلك الا باستخدام هندسة ريمان!
وهنا يظهر سؤال قديم جديد: هل هناك ما يمكن ان نطلق عليه العلم للعلم؟ فالبحث فى الهندسات الغير اقليدية كان ان لم يبدو وكأنه عمل مأفون فانه عمل بلا فائدة! ماذا لو لم يقم كل هؤلاء الرياضين بكل بهذا المجهود لاكتشاف الهندسات الغير اقليدية؟ الاجابة قطعا لم يكن لاينشتان ان يصل الى النظرية النسبية العامة!! وماذا لو لم يقم الاغريق فى البحث فى اشكال رياضية ليست ذات جدوى عملية واضحة كقواطع المخروط؟ اذن لم يكن لنيوتن أن ليتمكن من وضع قانون الجاذبية!
ومع هذا فان الباحثين فى هذه المواضيع الصعبة لا ينالون اى تقدير. فبولياى لم يلق اى تقدير فى حياته على اكتشافه للهندسة الغير اقليدية وكذلك لوبتشيفسكى فالتقدير اللذى حصل عليه كان لبحث له فى تطوير معالجة الصوف! ففى نظر المجتمع البحث فى شئ عملي كتصنيع الصوف اهم من اكتشاف هندسة جديدة. وعمل يحتاج الى ذكاء حاد وبصيرة نافذة وتجرد مذهل لا ينال تقديرا ماديا او ادبيا كما يناله تطبيق عملى بسيط.
ربما يجب علينا ان نضيف فى النهاية انه ليس كل ما يلمع ذهبا وعلينا دوما ان نحترم اصحاب العقول الكبيرة وان نقدر تجردهم وانجازهم حتى وأن بدا الامر اللذي يبحثون فيه انه بدون قيمة عملية. ربما اصدق تعليق حول هذا الموضوع ما قاله الخيام فى رباعياته:
عاشر مِن الناسِ كبار العقول
وجانب الجهّال أهل الفضول
واشرب نقيعَ السمّ مِن عاقلٍ
واسكب علَى الأرضِ دواء الجهول