رأينا في المرة الماضية نموذجا يحاكي انتشار فيروس كورونا باستخدام الدالة اللوجستية. وللتذكير فتلك الدالة تكون سرعة التغير فيها في البداية قليلة ثم تزداد حتى تبلغ قيمتها العظمي عند المنتصف ثم بعد ذلك تأخذ فى التناقص حتى تتوقف تماما. ولتبسيط ذلك نضرب مثالا ذئابا تسللت الى حظيرة خراف. فمتى تكون حصيلة الخسائر اكبر ما يمكن؟. لا شك ان الفتك يكون عظيما عندما تزداد عدد الذئاب المتسللة. ومن  ناحية اخرى تكون المقتلة اكبر عندما يزداد عدد الخراف الموجودة بالحظيرة. فاذا تخيلنا مثلا انه تسلل ذئبان الى الحظيرة وكان هناك خروف واحد. فلن نخسر خراف كثيرة. النتيجة اذن ان الخسائر تكون اكبر ما يكون بمعنى ان يكون معدل الخراف الهالكة فى الدقيقة اعلى مايمكن عندما تزداد عدد الذئاب وعدد الخراف في نفس الوقت.

دعونا نسقط ذلك المثال على عالم الفيروسات فهى مثل الذئاب اللتى تفترس ضحاياها. لكن الفارق ان الذئاب كائنات مستقلة بذواتها. اما الفيروسات فانها تعيش بداخل الكائنات الحية. ومن هنا نرى ان الفيروسات وحامليها ليسا منفصلين عن بعضهما. وبما ان عدد سكان المجتمع ثابت. فكلما زاد عدد الحاملين لفيروس قل عدد غير الحاملين  له وهم القابلون للعدوى في نفس الوقت. وفي بداية الوباء يكون حملة الفيروسات قليلين والقابلون للعدوي كثيرين فيكون معدل انتشار المرض بطيئا ومع مرور الوقت يصبح حاصل ضربهما اكبر ما يمكن ومن ثم تصبح سرعة انتشار الوباء عالية ثم يبدا الانحسار بعد ذلك.

دعونا نوضح ذلك بمثال رقمي: لو افترضنا ان لدينا مجتمعا مكونا من ستة اشخاص. فى البداية يكون عدد المرضى صفر وعدد الاصحاء ستة. اذن يكون المجموع الكلى ستة وحاصل ضربهم صفر. ثم يصبح لدينا مريض واحد وخمسة اصحاء فيبقى المجموع ستة ويزيد حاصل الضرب من صفر الى خمسة. فاذا زاد عدد المرضى واصبحوا اثنين ولدينا 4 اصحاء تصبح نتيجة الضرب ثمانية واعلى نتيجة ضرب نحصل عليها عندما يكون عدد المرضى يساوي عدد الاصحاء يساوي ثلاثة. فى هذه الحالة تصبحى نتيجة عملية الضرب تسعة. ثم يزداد عدد المرضى فيصبحون اربعة ويصبح عدد الاصحاء اثنين فمرة اخرى تقل نتيجة عملية الضرب وهكذا!

لكن  ماهي عيوب النموذج السابق ذكره؟. اولا هذا النموذج كما اي نموذج اخر هو اولا واخيرا نموذج اذن فهو خاطئ. لان اى نموذج هو كرسم كاريكاتير قائم على تعظيم عناصر معينة واغفال باقى العناصر الأخري. هذا من حيث المبدأ. اما من حيث التفاصيل فان نموذج الدالة اللوجستية خاطئ للعوامل التالية:

1 انه يضع فى الاعتبار عاملين فقط: وهما عدد الحاملين للفيروسات وعدد القابلين للعدوي بها أما باقى العوامل الاخرى فيتم اغفالها
2 انه يفترض ان سرعة انتشار المرض الأسية تبقى ثابتة. فماذا مثلا عن دور تغير المناخ ؟وهل انتشار المرض فى الصيف كما في الشتاء؟
3 انه يغفل اى دور يقوم به المجتمع للحد من انتشار ذلك المرض. كاجراءات التباعد الاجتماعى والحجر الصحي وما الى غير ذلك.
4 اعداد المرضى والوفيات هى اعداد صحيحة منفصلة ليست متصلة ولكن يتم تطبيق نماذج رياضية عليها خاصة برياضيات الأعداد الحقيقية المتصلة. لان أسلحة الرياضيات في هذا الميدان امضى وأقوى
5 عوامل اخرى

واليوم سوف نرى نموذج جديد يحاول ان يعالج بعض العيوب السابقة . وهو نموذج SIR وهو اختصار للكلمات التالية:

S من Suceptible وتعنى القابلين للعدوى
I من Infected وتعني المرضى اللذين يقومون بالعدوي
R من Recovered وتعنى اللذين  تخطوا مرحلة المرض

وهذا النموذج هو النموذج اللذي يستخدمه الرياضيون المحترفون عندما يرسمون سيناريوهات انتشار وباء ما. ولهذا النموذج تفريعات متعددة متنوعة اكثر تخصصا وتعقيدا. لكننا سوف نرى اليوم النموذج الرئيس فقط اللذى يوضح فكرة عمل هذا النموذج في العموم

في هذا النموذج نوزع سكان المجتمع على ثلاث شرائح. وهم اللذين ذكرناهم عاليا. ويمكننا توضيحهم كالتالى:

1 مجموعة القابلين للعدوى وقد يصاب احد افرادها بالعدوي وينتقل الى شريحة االمرضي
2 سرعة مرضهم هى كما في مثال الذئاب والخراف تزداد كلما زاد عدد الحاملين للفيروسات وعدد القابلين للعدوي في نفس الوقت. ويمكننا ان نعبر عن ذلك بالمعادلة التالية
S’ = -alpha * S * I
حيث S’ هو معدل مرض القابلين للعدوى فى وحدة الزمن و alpha هو ثابت و S هو عدد القابلين للعدوى و I هو عدد حاملى الفيروسات والاشارة السالبة توضح ان عدد الاصحاء دوما فى تناقص
3 يتعافى المرضى او يموتون بعد مرور فترة من الزمن وينتقلون من شريحة المرضى الى الشريحة R اللتى قد ترمز الى المتعافين Recovered او المزاحين من الحياة  Removed فللمفارقة اللذين يقضون بسبب الفيروس لا نعدهم مازالوا مرضى ولا نعدهم من القابلين للعدوي ولكن نحسبهم مع اللذين تخلصوا من المرض
4 معدل تعافى المرضى في وحدة الزمن يبتناسب مع اعدادهم ونرمز الى ذلك بالمعادلة البسيطة التالية
R’= beta * I
حيث بيتا هو ثابت
5 شريحة المرضى هى الشريحة الوحيدة اللتى يتدفق عبر جانبيها افراد من الشريحتين الاخرتين. فهى تستقبل افرادا من جماعة الاصحاء سابقا وتفقد عناصرها مع مرور الزمن لصالح شريحة المتعافين. وينبطق على معدل تغيرها المعادلة الأتية
I’ = alpha * S * I -beta *I
6 لا يوجد اتصال مباشر بين شريحتى القابلين للعدوي S والمتعافين R بدون المرور على شريحة المرضى I

اذن دعونا نعيد مرة اخري تقديم الثلات المعادلات السابقة:
S’=-alpha * S * I
I’=alpha * S *I – beta * I
R’ = beta * I

نرى في المعادلات السابقة ثابتين هما الفا وبيتا. فدعونا نري كيف يمكننا ان نحدد قيمتهما. لنبدأ اولا ببيتا حيث انه الاسهل. لو افترضنا ان فترة مرض الكوفيد 19 هى اربعة عشر يوما في المتوسط. اذن فالثابت بيتا يساوي واحدا مقسوما على 14. لنوضح ذلك بالمثال التالى لو أفترضنا انه مرض اليوم 28 شخصا بهذا المرض. فبعد 14 يوما فى المتوسط سيتعافون تماما. وبالطبع هذا لا يحدث فى قفزات كمومية. بل نفرض انه يحدث بنسبة ثابتة  يومية -1/14من عدد المرضى الكلي. بمعنى ان كل يوم يتعافى شخصان . فيصبح بعد يوم هنا 26 مريضا وبعد يومين 24 مريضا وبعد اسبوع اربعة عشر مريضا وبعد اسبوعين صفرا من المرضي. أذن بيتا تساوي بصورة تقريبية قسمة واحد على زمن الشفاء او المعادلة التالية
Beta = 1/ Recovery time

هذا عن الثابت بيتا. لكن ماذا عن الفا؟ في الحقيقة ان تحديد الفا اكثر تعقيدا. وهناك طريقة تقريبية ساقدمها هنا. وهناك طرق تقريبية اخرى سوف اتحدث عنها لاحقا. الطريقة هي اننا نعتبر ان سلوك الدالة فى البداية يشبه الدالة الاسية. واللذي يخضع للمعادلة التالية.
I(t)=I(0)*e^(alpha * N*t)
حيث  N هو عدد افراد المجتمع . ومن خلال العشرة ايام الاولى مثلا نستطيع ان نحدد قيمة الثابت الفا. ولاثبات ذلك رياضيا دعونا نوضح  التالي:
في البداية يكون عدد المتعافين صفرا
ويكون عدد المرضى قليلين
ويكون غالبية افراد المجتمع منتمين الى شريحة القابلين للعدوي.

انطلاقا من النقاط السابقة وخاصة ان عدد المتعافين يساوي صفرا فى البداية تكون بيتا تساوي صفر
ومنها يتبقى
I’ = alpha *S *I
واذا افترضنا ان عدد سكان المجتمع N فانهم سيكونون موزعين على شريحتى المرضى والقابلين للعدوي فقط. ومن هنا
I’ = alpha*(N-I)*I
وهذه هي معادلة الدالة اللوجستية كما رأينا المرة الماضية.
دعونا الان نجري تقريبا جديدا حيث نفترض انه فى البداية عدد المرضى يكون قليلا بحيث يكون N-I يساوي تقريبا N فلو طرحنا 10 من مائة مليون فان النتيجة سوف تبقى عمليا مائة مليون. ومن هذا
I’= alpha *N  *I
اوبما أن الفا وN هما ثابتان نرى ان معدل تغير عدد المرضى الاني يتناسب طرديا مع عدد المرضى وهذا هو شرط الدالة الاسية كما تعرفنا عليه فى المرة الماضية. وهذا هو البرهان اللذى نسعى اليه

اذن وبعد تحديدنا للثوابت الفا وبيتا كيف يمكننا ان نحل المعادلات التفاضلية الثلاثة السابقة؟ في الحقيقة ان المعادلات التفاضلية السابقة ليس لها حل صريح. ولكن هناك بعض الطرق التقريبية للتعامل مع هذه المسألة. دعونا نرى اسهل هذه الطرق وابسطها وهى تعرف بطريقة اويلر

هذه الطريقة مبنية على ان نستخدم متوسط التغير فى فترة زمنية ضيقة على انه معدل التغير الاني. وطبعا لا يمكنك ان تصارح بهذا متخصصا فى الرياضيات البحتة ولا يقوم بالانتحار. لان هذه الفرضية خاطئة تماما. اما المتعاملون فى الرياضيات التطبيقية فيعلمون ايضا ان هذا الافتراض خاطئ. لكن السؤال العملى ما هى قيمة  هذا الخطأ؟ وهل يمكننا ان نتعايش معه او لا؟ وخاصة اننا لانريد فعلا تحديد عدد المرضى تحديدا دقيقا صارما . ولكننا فى الاول والاخير نبحث عن مؤشرات لتفشى مرض و نريد ان نقارن بين اجراءات الوقاية المتباينة. وحيث اننا فى موضوعنا نفترض ان وحدة الزمن هى اليوم. فانني سوف اقسم اليوم الى 1440 قسما وهى عدد الدقائق الموجودة فيه واحسب متوسط التغير فى كل دقيقة. طبعا هنا سوف نجرى عمليات حسابية كثيرة جدا وسوف نحتاج الى جهاز كمبيوتر ولكن عزاؤنا اننا سوف نقلل الخطأ الى اكبر درجة ممكنة

دعونا الان نرى مثالا حسابيا. اذا افترضنا وجود قرية او مدينة صغيرة عدد سكانها عشرة الاف شخصا. وان هناك مائة شخصا اصيبوا بمرض كوفيد 19 . ولنفترض ان فترة التعافى من هذا المرض فى المتوسط هى اربعة عشر يوما ستكون بيتا تساوي واحد مقسوما على 14 . اما الفا فلنفترض اننا حددنا قيمتها ب 0.0000214 اذن باستخدام برنامج الاكسل Excel او اي برنامج اخر مقارن له نستطيع ان نجري العمليات التالية
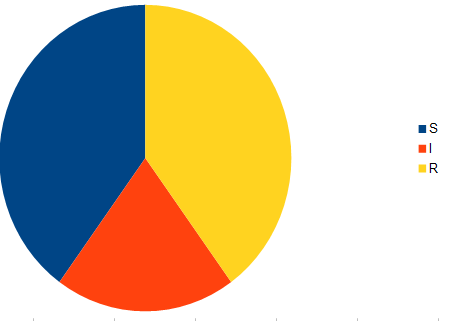
R=0
I=100
S=9900
ثم نكرر الخطوات التالية حتى تصبح قيمة I صفرا اى ان المرض سوف يزيد ثم ينحسر
S =S -alpha *S*I /1440
I = I + alpha * S*I /1440 – beta *I/1440
R = R +beta * I/1440
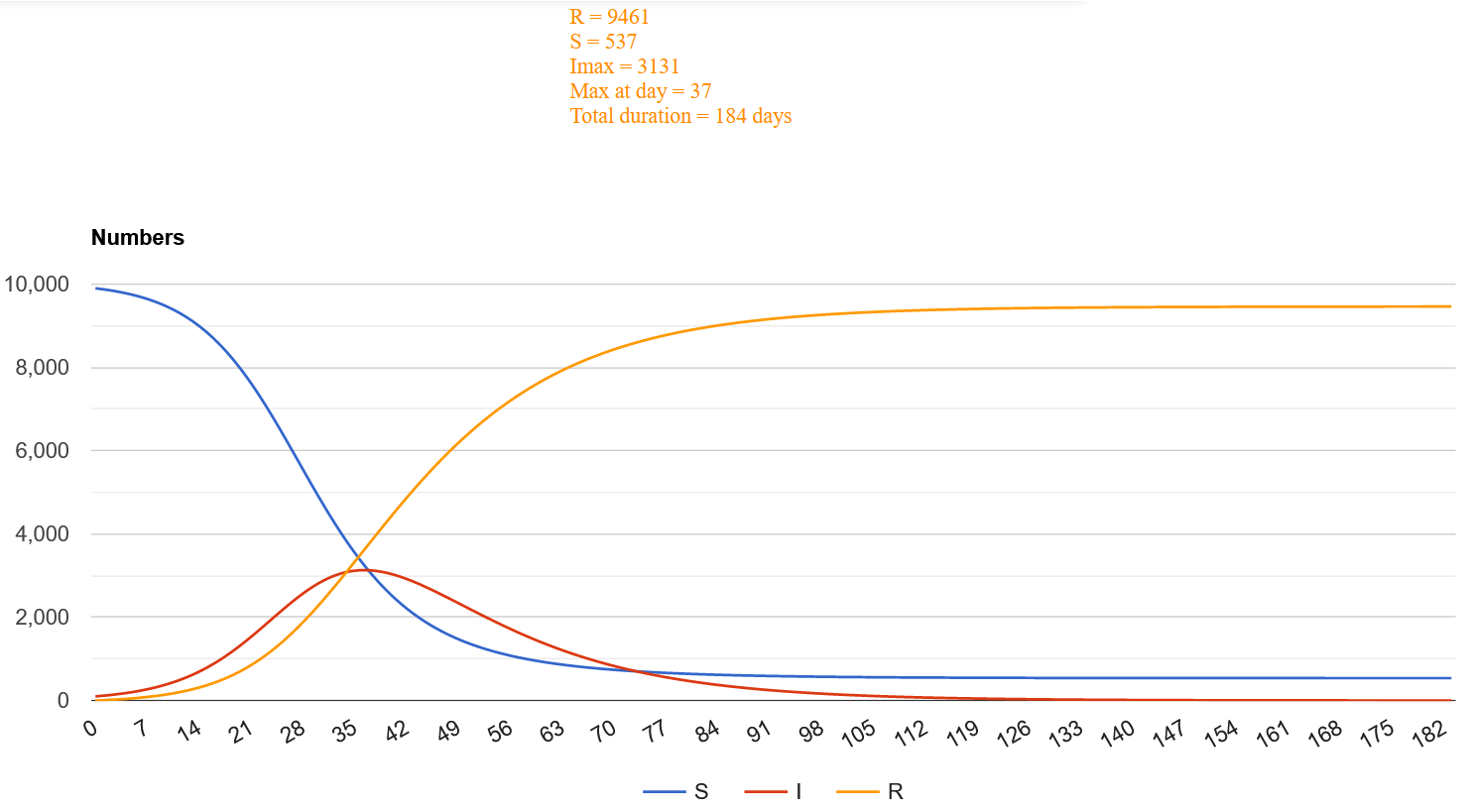
وبتطبيق هذه الطريقة على مدينتنا سنجد ان الوباء سيتوقف بعد ان يصاب به 94% من كل سكان المدينة وبعد زمن قدره 184 يوم أما أعلى نسبة للأصابات فانها ستكون بعد 37 يوما حيث سيكون 31% من سكان تلك المدينة مرضى في يوم واحد.

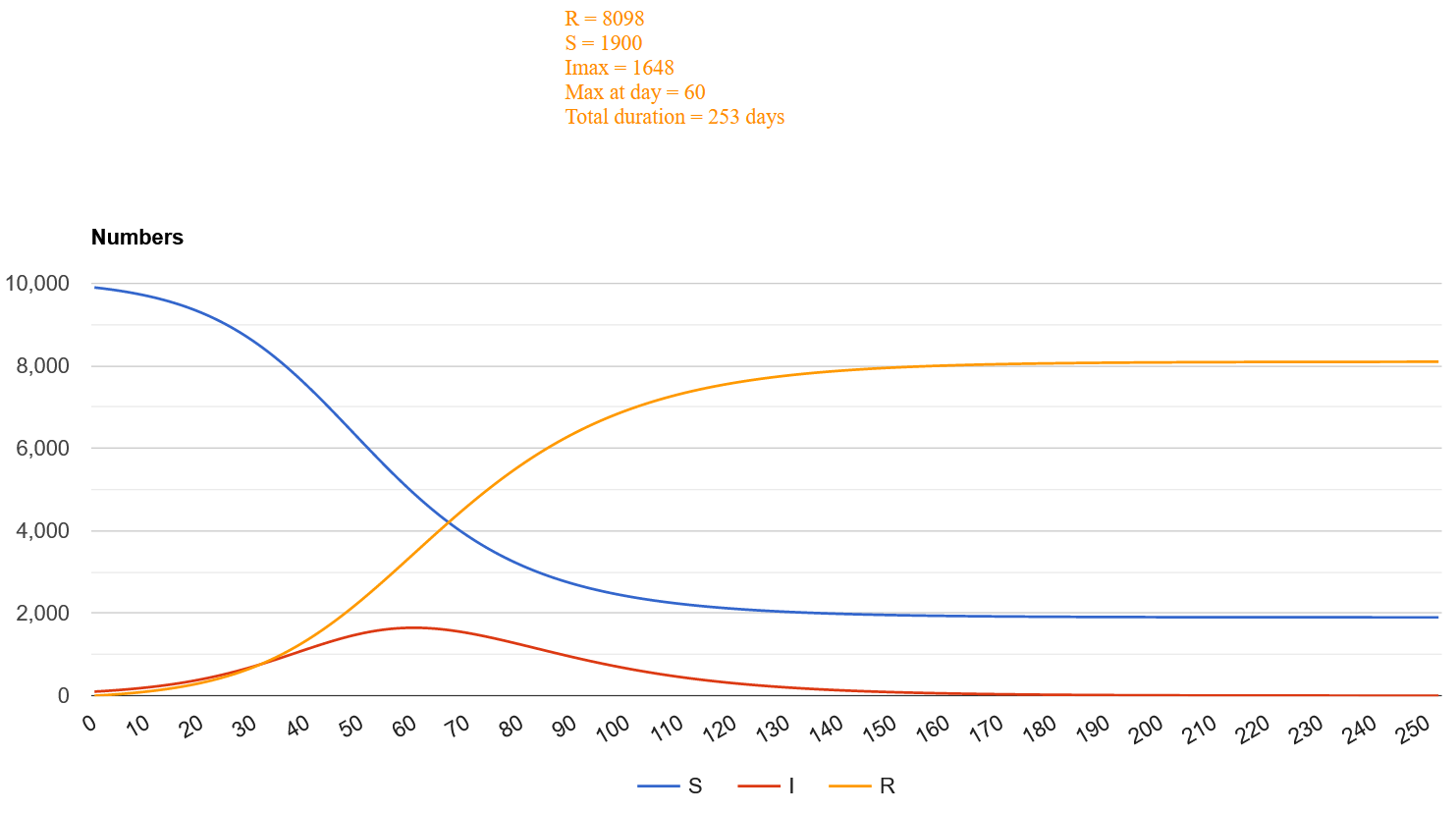
واذا اعدنا نفس الحسابات مرة اخري لكن بافتراض اننا باجراءات التباعد الاجتماعى وعمليات التقعيم والنظافة استطعنا تخيفيض قيمة الفا الى ثلثي القيمة فسيتوقف الوباء بعد ان يصاب به 80% من افراد المجتمع وبعد زمن قدره 253 يوما. اما اعلى نسبة للاصابات فانها سوف تكون 16.5% فقط وذلك بعد مرور 60 يوما. وهذه نتيجة هامة جدا. اذ اننا خفضنا قيمة الفا الثلت فقط فكانت النتيجة ان انخفضت قمة الاصابات اليومية الى النصف تقريبا. وهذه الحيلة هى ما يطلق عليها تسطيح المنحنى او Flatten the curve

الان وبعد ان رأينا كيف تعمل هذه الطريقة. دعونا نتأمل بشيئ من التمعن تفاصيلها وفي معانيها اللتى تحملها. ربما يكون  السؤال الاهم ماهي الشروط  الرياضية اللتى يتوفرعندها وباء؟ الاجابة الواضحة طبعا عندما يكون معدل تغير الاصابات بالنسبة للزمن اكبر من الصفر. حيث انه عندما يكون سالبا تأخذ اعداد المصابين فى التناقص. اذن يكون عندنا وباء عندما يكون:

I’=alpha * S * I – beta * I > 0
ومنها
alpha * S * I > beta * I
أو
alpha * S /beta > 1
دعونا ندخل الان متغيرا جديدا R تعريفه كالتالى
R = S* alpha/beta

وذلك المتغير الجديد فى غاية الاهمية وهو يعرف ب Effective Reproduction Number
وعندما يكون اكبر من واحد يكون عندنا وباء وتكون اعداد المرضى في ازدياد مستمر وعندما يكون العدد اصغر من واحد يكون الوباء فى انحسار شديد. دعونا الان نتعرف على عناصر R بشيئ من التمحيص. دعونا نصف ذلك بالكلمات:

R هى حاصل ضرب الفا في عدد الافراد القابلين للعدوي ثم نقسم النتيجة على بيتا!! ما معنى ذلك؟ دعونا نفعل ذلك خطوة خطوة. ما معنى الفا؟ من التعريف:
S’ = alpha *S*I
دعونا نتتبع ذلك عندما يكون لدينا مريض واحد فقط. اى اننا نعوض فى I ب واحد. اذن
S’ = alpha *S
أو
alpha = S’/S
او بالكلمات الفا هى ناتج قسمة معدل مرض الافراد القابلين للعدوي فى وحدة الزمن مقسومة على عدد الافراد القابلين للعدوي عندما يكون هناك مريض واحد. او بصياغة اخرى هى عدد الاشخاص اللذين تمت اصابتهم بالعدوي فى يوم واحد من قبل شخص واحد مقسومة على عدد القابلين للعدوي.

ربما تكون القسمة على عدد الاشخاص القابلين للعدوي امرا محيرا وسخيفا. لكن لا بأس. فنحن فى الخطوة الثانية نضرب الفا فى S أى اننا نختصر عدد الاشخاص القابلين للعدوى خارج المعادلة ليصبح معنى عملية الضرب حتى الان هو عدد الاشخاص اللذين يتم اصابتهم بالعدوي من قبل شخص واحد في يوم واحد

لكن ماذا تعنى القسمة على الثابت بيتا؟ دعونا نتذكر اننا عرفنا الثابت بيتا على انه المقلوب العددي للأيام اللتى يقضيها المريض مريضا. فالقسمة على هذا المقلوب تعنى اننا فى الحقيقة نضرب فى عدد الايام اللتى يقضيها المصاب مريضا فى المتوسط. ومن هنا نحصل على تصور لقيمة R على انه عدد الاشخاص اللذي يصيبهم شخص مريض بالعدوي طوال فترة اصابته فى المتوسط.

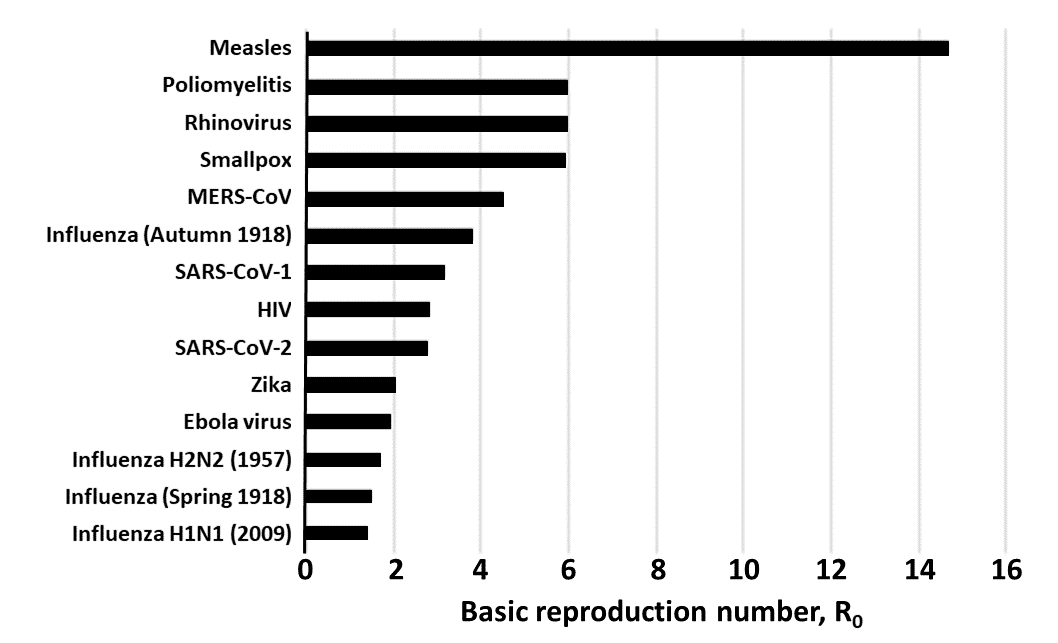
ولذلك الثابت اهمية كبير وهناك قيمة خاصة لهذا المتغير في اول الوباء تعرف ب أر صفر R_0 وهى تعنى متوسط عدد الاشخاص اللذين يصيبهم المريض رقم صفر فى اول الوباء . وهذه القيمة فى غاية الاهمية. وبالنسبة لمرض الكوفيد فقد حدد الصيينون هذه القيمة بثلاثة وكذلك فعل الالمان. اى ان الشخص المصاب يقوم بعدوى ثلاثة اشخاص فى خلال فترة مرضه. اما الامريكيون فقد حددوا هذ القيمة بخمسة.

دعونا مرة اخرى نتأمل في معنى هذه القيمة. اذا كانت هذه القيمة اكبر من واحد فتعنى ان عندنا وباء. لكن لماذا؟ لنفرض انه هذه القيمة تساوي ثلاثة. اي ان اول انسان مريض يصيب ثلاثة اشخاص بالعدوي. ثم يشفى هذا المريض. لكنه يترك ثلاثة مصابين خلفه لانهم قد مرضوا بعده وبالتالى سوف يشفون بعده. ثم يقوم كل شخص من هؤلاء الثلاثة بنقل العدوي الى ثلاثة اشخاص اخرين قبل ان يشفى هو. فتكون النتيجة ان يشفى هؤلاء الثلاثة ولكنهم يتركون خلفهم تسعة من الحاملين للعدوي الجدد. وتستمر تلك العملية فى الانتشار . ومن هنا نرى ذلك الانتشار الأسي.

اما اذا كانت تلك القيمة اقل من واحد مثلا لنقل انها نصف. فكل اربعة اشخاص مثلا سينقلون العدوي الى شخصين فى المتوسط. ثم يشفى هؤلاء الاربعة ويتبقى الاثنان الجدد فقط. ثم يقوما هذان الاثنان بنقل العدوى الى شخص جديد قبل ان يشفوا. وبذلك يتبقى لدينا مريض واحد فقط. وبهذا نرى ان المرض يكون فى انحسار سريع وبشكل أسى كذلك

أما الحالة الخاصة عندما يكون R يساوي واحد. اى ان كل شخص مريض يشفى بعد ان ينقل المرض الى شخص اخر. وبهذا نجد ان المرض لا ينتهى ولكنه لا يزداد ايضا بصورة اسية. وهذا على سبيل المثال ينطبق على الاستراتيجة الالمانية الحالية لمكافحة مرض الكوفيد حيث انهم بعد ان خفضوا عدد المصابين بهذا المرض يريدون ان يبقوا هذا العدد عند القيمة واحد. اى ان يقوم كل شخص مريض بنقل العدوي الى شخص واحد فقط وبهذا يبقى المرض موجودا دائما ولكنه يبقى دوما تحت السيطرة. دون الحاجة الى القيام باجراءات حظر صحى قاسية لان هذا يضر بالاقتصاد. وسوف نتحدث عن هذا لاحقا.

فى الحقية ان الرقم ار صفر يساوي ثلاثة فى حالة الكوفيد 19 ويعتبر قيمة عالية تبين ان المرض له انتشار سريع فعلا. لكن هذ القيمة ليست اعلى القيم المعروفة بين الامراض المختلفة. ففى حالة مرض الحصبة  فان هذه القيمة تساوي 15. اي ان المريض يقوم فى المتوسط بنقل العدوي الى 15 شخصا اخر قبل ان يشفى هو.

وهناك طرق عديدة لتحديد هذا الرقم عمليا. من هذه الوسائل نذكر الطرق التالية.

في بداية العدوي قام الصينيون بتحديد هذه القيمة عن طريق تحريات استقصائية. حيث انهم قاموا باستجواب حوالى 500 مريض. عن كيفية انتقال العدوي اليهم والى من قاموا هم بنقل العدوي ووجدوا انه هذا القيمة تساوي فى المتوسط ثلاثة.

وهنا طريقة ثانية وهى الطريقة اللتى يتبعها الالمان حيث انهم يقومون باحصاء عدد حالات العدوي الجديدة فى الايام الاربعة الاخيرة. ثم يقومون بقسمة هذه النتيجة على اعدد المرضى الجدد فى  الايام الاربعة السابقة لهم. والمغزى فى هذا . ان عدد الايام اللتى يكون فيها الانسان معديا هى فى المتوسط اربعة ايام. والفكرة ان من تمت اصابتهم بالعدوي فى الايام الاربعة الاخيرة قد انتقلت اليهم العدوي عن طريق هؤلاء المرضى الجدد فى الايام الاربعة السابقة لذلك

وهناك طريقة ثالثة منبعثة من تعريف R نفسه حيث اننا نقوم هنا بتحديد قيمة الفا وبيتا كما رأينا سابقا. واحصاء عدد الافراد القابلين للعدوي حاليا امرا ليس صعبا حيث انه يساوى عدد افراد المجتمع مطروحا منه عدد الاشخاص الكلى اللذين انتقلت اليهم العدوى حتى الان ثم نقوم كما التعريف بضرب هذه القيمة فى الفا ثم قسمة النتيجة على بيتا.
R = alpha * S / beta

الان دعونا نري العوامل اللتى نستطيع من خلالها ان نجعل قيمة R أقل من واحد.

اول تلك العوامل وهو عدد القابلين للعدوي . فى البداية كما رأينا يمكننا ان نفترض ان عدد سكان المجتمع في البداية كلهم قابلين للعدوي. ولنفترض ان قيمة الابتدائية هى ثلاثة كما هو مشهور عن فيروس كورونا الجديد.  الان بعد مرور الزمن واصابة ثلثين المجتمع بالعدوي. فان عدد القابلين للعدوي سيقل تلقائيا ويصبح ثلث القيمة السابقة . ومن هنا ينخفض الثابت الى القيمة واحد مما يعني ان الوباء الان سيأخذ فى التناقص. وهذه الظاهرة هى ما يطلق عليها العلماء ذلك اللفظ اللذى ربما قد سمعها معظمنا وهو مناعة القطيع. واللذي يعنى باختصار ان بعد اصابة قطاع لا بأس به من المجتمع – فى حالة كورونا ثلثي المجتمع تقريبا- . فان الوباء سيأخذ فى الانحسار. لكن علينا طبعا ان نلاحظ ان انتشار الوباء لن يتوقف فى التو واللحظة عند وصول الاصابات الى ثلثى المجتمع. لكن ذلك يعنى فقط ان الوباء سوف يأخذ من هذه اللحظة فصاعدا فى التوقف السريع. وراينا فى المثال السابق فى المدينة الصغيرة ذات العشرة الاف ساكنا فى الحالة الاولى واللتى كانت قيمة R فيها ثلاثة -وان لم اصرح بذلك فى تلك اللحظة- وراينا ان الوباء سيتوقف بعد ان اصاب 94% من المجتمع.

وربما سمع معظمنا باستراتيجية مناعة القطيع لمكافحة وباء كورونا. وهذه الطريقة تبدو على الورق سهلة ومغرية. فكما رأينا من المثال الثاني انه قللنا قيمة R الى 2 فان المرض سينتهى اذا تعرض 80% من المجتمع للاصابة بالعدوي. وفى نفس الوقت نعلم ان 85% من حالات الاصابة تتم بلا اية اعراض نهائيا او باعراض بسيطة فقط. بينما من يعانى من هذا المرض بشكل متوسط او قوي هم 15% فقط من افراد المجتمع. اذن الحل يبدو سهلا ان نعرض فقط هؤلاء ال85% اللذين يتلقون الصدمة بسهولة للمرض فلا يحدث لهم شيئ وفى نفس الوقت نكون اوقفنا انتشار المرض نهائيا. ومهمة الجهات المختصة في هذه الطريقة نشبهها كما فى حالة تخصيب اليورانيوم هى فصل شرائح المجتمع المعرضة للخطر من مرض الكوفيد 19 عن الشريحة الاكبر اللتى تستطيع ان تتجاوز الاصابة بكل سهولة. وتعريض فقط تلك الشريحة للاصابة وعزل الطائفة الضعيفة عزلا مستحكما. وسوف نتحدث مرة اخرى حول هذه الاستراتيجية بعد قليل.

وهناك طريقة اخرى فى غاية الاهمية نستطيع ان نقلل بها عدد القابلين للعدوي بدون جعلهم يمرضون أولا وذلك عن طريق اكتشاف لقاح. ففى هذه الحالة نستطيع مثلا ان نقلل عدد القابلين العدوي الى الثلث عن طريق تطعيم ثلثى المجتمع وبهذا نفرمل انتشار المرض مباشرة

اما العنصر الثاني الداخل فى حساب R هو بيتا اللذي نقوم بالقسمة عليه. وكما رأينا سابقا ان معنى تلك عملية القسمة اننا  نضرب عمليا فى زمن المرض. اذن نستطيع ان نقلل من قيمة R اذا استطعنا تخفيض فترة علاج المرض. وذلك عن طريق اكتشاف دواء فعال. لكن يبدو ان التأثير عبر هذا العنصر صعبا. فكما رأينا الغالبية الساحقة من الحالات تمر بلا اعراض او باعراض بسيطة لا يحتاج فيها المصابون الى اى علاج ولا يذهبون الى الطبيب. صحيح ان هناك عقاقير تم اكتشافها تستطيع ان تخفض فترة البقاء فى المستشفى فى كثير من الحالات من 15 يوما الى 11 يوم. لكن يبقى في النهاية هذا الطريق بدون فاعلية كبيرة

اما العامل الثالث اللذي يدخل فى صناعة R هو قيمة الثابت الفا وهذا العامل هو اللذي تلعب كل الدول على التأثير عليه. عن طريق اقرار قوانين النظافة وارتداء الكمامات والتباعد الاجتماعى.

الان وقبيل النهاية نعلم ان ايى نموذج هو صحيح بقدر صحة الافتراضات الداخلة فى بناءه. دعونا مرة اخرى نستعرض الافتراضات اللتى افترضناها فى طريقتنا اليوم ونقاط ضعفها:

النقطة الاولى هى  انها تفترض ان عدد سكان المجتع ثابت وان الافراد ينتقلون فقط من شريحة الى اخرى. ولا تراعي الطريقة زيادة عدد سكان  المجتع عن طريق الولادة ونقصه عن طريق الوفاة بطريقة ليست لها علاقة مباشرة بالوباء تحت الدراسة ولا تراعي عمليات الهجرة والنزوح بين ومن المجتمعات.

النقطة الثانية كما فى الموضوع السابق انها تستخدم تقنيات الاعداد الحقيقية المتصلة فى موضوع يتعلق باعداد صحيحة منفصلة. فلا معنى لان يموت او يمرض 19.5 مصابا مثلا.

النقطة الثالثة اننا نحسب قيم الثوابت بيتا وألفا ونحل المعادلات التفاضلية بطرق تقريبية

النقطة الرابعة اننا نفترض ان طوال فترة المرض يبقى الانسان معديا. لكننا نعلم ان الفترة اللتى يكون فيها الانسان معديا لاتساوي بالضرورة فترة مرضه. ففي حالة الكورونا مثلا يبقى المرض في المتوسط حوالى اسبوعين ولكنه لا يكون  معديا لغيره الا فى خلال اسبوع واحد فقط علي الاغلب

النقطة الخامسة انها تفترض ان بعد المرض يكتسب المريض مناعة تبقى مدي الحياة. لكن هذا ليس صحيحا دائما

النقطة السادسة  انها تعتبر ان كل البشر متساوون من حيث النشاط و في استطاعتهم نشر المرض لغيرهم. لكن نعلم ان هذا الفرض ليس صحيحا فالاطفال اللذين يذهبون الى المدراس هم اكثر ناس يختلطون بغيرهم وبطوائف اخرى من المجتمع ومن هنا هم ربما يكونون اكثر الناس نشاطا فى نشر المرض. ثم هناك طائفة الشباب اللذىن يتحركون كثيرا فى المجتمع ويختلطون كثيرا بغيرهم. هؤلاء ايضا يستطيعون ان يساهموا فى نشر المرض بشكل سريع على خلاف الكبار فى العمر

النقطة السابعة ان الاختلاط بين البشر ليس كاملا فلا يستطيع ان يصل كل انسان الى أي انسان اخر فالناس يسكنون جغرافيا فى مناطق مختلفة. صحيح ان وسائل المواصلات تطورت كثيرا. لكن مع ذلك فان الاختلاط الكامل بين كل سكان العالم او كل سكان دولة ما او حتى مدينة كبيرة ما ليس ممكنا

لكن فى نفس الوقت فان ماعرضناه اليوم ليس الا الطريقة الاساسية من التقنية ٍوهناك تفريعات مختلفة نستطيع ان نحل بها كثير من الاعتراضات اللتى سردناها عاليا فهناك صور كثيرة منقحة من الطريقة الاساسية كالتالي

هناك صور تفترض ان عدد سكان المجتمع ليس ثابتا وتستطيع ان تعالج التغير في عدد سكان مجتمع ما عن طريق عمليات الولادة والوفاة والهجرة

هناك صور تستطيع ان تتعامل مع حقيقة ان فترة المرض لا تساوي فترة العدوي بالضرورة وذلك باضافة شريحة رابعة الى النموذج للمرضي اللذين لا ينقلون العدوي الى سواهم

وهناك صور تستطيع ان تتعامل مع ان المناعة ليست ابدية. وفى هذه الصورة ينتقل فيها الافراد من المجموعة R الى المجموعة S مرة اخرى

هناك صور تستطيع ان تتعامل مع التوزيع الجغرافى للبشر ومعيشتهم فى كثافات سكانية مختلفة

فى النهاية هنا ينتهى الحديث العام عن هذه الطريقة واحب ان استعرض في الاسطر القادمة مجهود شخصى او برنامج قمت ببرمجته يحاكي باستخدام النموذج السابق انتشار مرض الكوفيد 19 في دول العالم المختلفة. ولا ادعى ان هذ النموذج دقيق فكل ماهو بيدي هو اعداد الوفيات والاصابات حول العالم اللذى تنشره الكثير من المنصات الالكترونية على شبكة الانترنت. والنقاط التالية اود ان اسلط الضوء عليها

https://eltawil.org/corona_modelling/logistic_function/index2.php

اعلم ان رصد حالات الاصابات من الجهات المختصة ليس سهلا. فاكثر من 50% من المصابين بالفيروس لا يصابون باى اعراض نهائيا ولا يذهبون الى اي طبيب. كما ان هناك نسبة لا بأس بها تظهر عليهم اعراض طفيفة فقط وهم من هذا المنطلق يشبهون المجموعة السابقة. بل وحتى ان الاعراض لاتظهر فورا بل يمر اسبوع في المتوسط قبل ان تظهر اية اعراض. فبالتالى اى دولة مهما كانت كفائتها لا تستطيع ان تحصي الاعداد الحقيقية للاصابات. والنقطة الثانية ان معظم دول العالم ليست كفؤة من  الاساس وليست لها القدرة على اجراء اختبارات كافية فى زمن مناسب. وهناك نقطة اخرى ان كثير من الدول لا تتمتع بالشفافية وربما تكون لديها الرغبة في عدم قول الحقيقة بشأن  انتشار المرض بين ابناء شعبها

اذن من الخليط السابق من صعوبة الحصول على الارقام الحقيقية وعدم كفاءة معظم الدول من الاساس وميل كثير منها الى عدم قول الحقيقة. فاننى لم اخذ الارقام اللتى تعلنها الدول عن عدد الاصابات لديها على محمل التصديق وبحثت عن طريقة اخرى استطيع ان احصل من خلالها على ارقام اكثر دقة

وهنا قررت الاعتماد على اعداد الوفيات كمصدر غير مباشر للحصول على اعداد الاصابات. حيث ان احصاء اعداد الوفيات الاقل اكثر سهولة من احصاء حالات الاصابة. لكنى اعلم ايضا ان هناك الكثير من الحالات اللتى تحدث الوفاة فيها بسبب مرض الكوفيد ولا يتم رصدها. لكننى أفترضت ان الخطأ هنا لا بد وان يكون اقل من حصر الاصابات مباشرة

اي اننى فى الحقيقة استخدم نموذجين : الاول هو موضوع مقالة اليوم والثانى هو نموذج للحصول على اعداد الاصابات بمرض الكوفيد 19 بدلالة اعداد الوفيات

هناك دراسة قامت بها جامعة المانية فى مدينة أنتشر بها المرض بشكل قوي ووجدت ان نسبة الوفيات هى 0.38% من عدد الاصابات الكلية. وهناك ايضا ألابحاث اللتى اجريت على السفينة دياموند برنسيس وهى سفينة سياحية اصابت الجائحة الكثيرين من الموجودين عليها وتم حجر تلك السفينة بالكامل وكان عدد الموجودين على السفينة بضعة الاف وتمت اجراء الاختبارات على جميع الموجودين اكثر من مرة. وتم تحديد تماما من لم يصيبوا بالمرض ومن اصيبوا ولكن بلا اعراض ومن اصيبوا باعراض ومن ماتوا. وكانت نسبة الوفيات الى الاصابات بعد اجراء بعض التعديلات الاحصائية هى ايضا 0.38% بمعامل دقة لا بأس به فاعتبرت ان هذه النسبة هى قيمة ثابتة من اجمالى الاصابات

لفت نظري ايضا ان هناك دول مع ذلك نسبة الوفيات فيها اقل من نسبة الوفيات في الدول الاخرى. هذا ينطبق مثلا على الدول العربية. فعدد الوفيات مثلا فى مصر اقل منه في المانيا والسبب غير معلوم. ربما يكون السبب هو المناخ أو اختلاف التركيبة الديموجرافية حيث ان نسبة  الشيوخ وكبار العمر فى الدول العربية منخفضة بالمقارنة باوروبا. وربما يكون الامر له علاقة باختلاف اللقاحات اللتى تلقاها الافراد هنا وهناك. خلاصة الامر ان السبب الحقيقى لا يهمنا هنا. ولكنى افترضت وجود نوعين من البلاد. الاولى نسبة الوفاة فيها هى 0.38% اما الثانية فافترضت ان نسبة الوفياة فيها هى 0.13% وهى نسبة كبيرة ايضا وتساوي نسبة الوفيات جراء الانفلونزا

ولسهولة الحسابات فى النقاش التالى سأفترض ان نسبة الوفيات للاصابات هى فقط 0.1% فمعنى وجود حالة وفاة واحدة هى وجود 1000 حالة اصابة. ونحصل على عدد الاصابات عن طريق قسمة عدد الوفيات على هذه النسبة اللتى ذكرتها عاليا

لكن حتى حدوث حالة وفاة في يوم وبناء الف حالة اصابة عليها لا يعنى ذلك ان هؤلاء الالف شخص تمت اصابتهم في نفس اليوم. بل نلاحظ التالى. يمرض الانسان اولا فى وقت ما فيبقى اسبوع فى المتوسط بلا اى اعراض. ثم تظهر عليه اعراض تجبره الى الذهاب الى المستشفى ويبقى هناك فى المتوسط عشرين يوما حتى تحدث الوفاة. ثم تحدث اجراءات ابلاغ حالة الوفاة من الجهات المحلية الى الجهات الاعلى منها حتى يصدر الاعلان رسميا عن الوفاة في النهاية ان وفاة شخص اليوم تشترط حدوث اصابة الف شخص 28 يوما قبل ذلك فى المتوسط

ونفس المنطق ينطبق على اعلان حالات الاصابة. فالانسان يبقى اسبوع بلا اعراض ثم تظهر عليه بعض الاعراض فيذهب الي طبيب اللذي يجري عليه فحص وتاخذ نتيجة الاختبار بضعة ايام حتى تظهر النتيجة ويتم اعلانها. وهنا افترضت ايضا مرور 10 ايام على حدوث الاصابة فعليا قبل اعلانها فى المتوسط.

فاذا حركنا اعداد الوفيات 28 يوما الى الخلف واعداد الاصابات 10 ايام الى الخلف. نجد ان هناك تقاطعا لابأس به بينهما لكن توجد ايضا فجوة 18 يوم بين نتائج الوفيات والاصابات الاحدث لاأستطيع من خلالها الاستدلال على عدد الاصابات بدلالة عدد الوفيات الا باستخدام نموذج ثالث

الان بالمقارنة بين اعداد الاصابات اللتى نحصل عليها عن طريق النموذج مع الاعداد المعلنة من قبل الدول في القسم المشترك بينهما نستطيع ان نتوقع الفارق بين الارقام الحقيقية للاصابات والارقام المعلنة ومن هنا ربما نستطيع ان نحكم على جودة نظام الاختبارات فى دولة ما. وهذا ما اطلقت عليه Infection-Case-Factor فنجد مثلا ان الفارق بين دول مشهود له بجودة اجراء الاختبار كالمانيا وكوريا الجنوبية ب 15 ضعفا. ويمكننا ان نعمم ونقول اذا كان الفارق أقل من 30 فان الدول تتمتع بنظام اختبارات جيد والا العكس

لحساب قيمة الثابت الفا واعلم ان قيم هذا الثابت قد تتغير عبر الزمن بناء على مجهودات الدول المختلفة لكبح المرض ويؤثر عليه مدي التزام الجماهير باجرائات الحظر والتباعد الاجتماعي. وقد يتعلق الامر بتغير المناخ وما الى غير ذلك. قمت باستغلال المعادلات وباكثر من طريقة
alpha =S’/(S*I)
alphs = (I’+beta * I)/(S*I)
وايضا من خلال تحديد قيمة R عن طريق قسمة عدد الاصابات فى الثلاثة ايام الاخيرة مقسومة على الثلاثة ايام السابقة لها ثم تطبيق المعادلة
alpha =R*beta/S

وكما راينا من مثال المدينة ذات العشرة الاف نسمة واللتى لم تتخذ اى اجراءات للحد من انتشار المرض فكانت نسبة الاصابات فيها 94% . هنا مرة اخرى نستطيع ان نرى قيمة المجهودات اللتى تقوم بها كل دولة ومدى نجاعة تلك الاجراءات في السيطرة على المرض عن طريق المؤشر Herd-Immunity . وهنا تظهر حساباتى ان افضل الدول العربية فى مكافحة هذ الوباء في صباح 21 مايو عام 2020 هى فى تونس ولبنان وفلسطين. وتظهر الحسابات ان دول الخليح تبذل مجهود ممتاز فى اجراء الاختبارات وافضل دول الخليج فى ذلك هى قطر. لكن اجراءات الوقاية لا يبدو انها ناجحة بالقدر اللازم. اما على مستوى العالم فان اكثر الدول نجاحا فى التعامل مع هذا المرض فهى دول شرق اسيا كتايوان وكوريا الجنوبية واليابان

اما عن اجراءات الحماية اللتى قد تقوم بها الدول للحد من انتشار تلك الجائحة فهى لا تخرج عن الوسائل التالية

الطريقة الاولى هى الاحتواء Containment وهذا الطريقة لم تنتهجها الا القليل من الدول واهمها الصين. وهذه الطريقة تهدف الى احتواء المرض وجثه كلية فى اسرع فترة زمنية ممكنة. وذلك قائم على اجراءات التقصى والتحريات والتتبع لكل حالات الاصابة وحجز المخالطين لها بمنتهى السرعة والحسم ومنع الاختلاط والاقفال التام لمناطق كثيرة اذا لزم الامر. ولكى تنجح هذه الطريقة فانها تشترط عدم تفشى المرض قبل اخذ الخطوات اللازمة والا سيصبح تتبع المرض مستحيلا. وهناك حد اقصى لعدد الحالات اللتى يسمح بوجودها حتى تنجح هذه الطريق وهو ليس رقما ثابتا بل يختلف من دولة الى اخرى وتعتمد على كفائة اجهزة الدولة فى عمليات التتبع والتقصى والحجز والحجر

الطريقة الثانية هى التخفيف Mitigation فقط وليس البتر الكامل للمرض وهذه الطريقة هى اللتى تتبعها معظم دول العالم. فهى تعلم ان المرض منتشر بها فلن تنجح اجراءات الأحتواء. كما ان تكلفة الاغلاق الكامل للدول عالية جدا لاتستطيع أي دولة اللجوء اليها لفترة طويلة. هذه الاستراتيجية تهدف الى الحد من انتشار المرض عن طريق التباعد الاجتماعى وارتداء الكمامات واتخاذ اجراءات النظافة والتعقيم والحجر الكلي او الجزئي لبعض الانشطة فى المجتع. والهدف هو تقليل حالات الاصابة الي الحد الادني واللذي ربما قد يسمح فى مرحلة قادمة باحتوائه وبتره نهائيا. وما يميز هذه الطريقة انها تسعى الى تاخير الاصابات فقط وليس منعها كليا وهو ما نطلق عليه تستطيح المنحنى. وهذا قد تكون له اكثر من فائدة اولها كسب الوقت حتى الوصول الى لقاح فعال يستطيع ان يغير المعادلة بشكل حاسم. الفائدة الثانية هو عدم تحميل الاجهزة الصحية الموجودة فوق طاقتها. فاذا اخذنا ايطاليا مثلا على سبيل المثال . نجد ان النموذج يقول ان عدد الحالات الموجودة بلغ اقصاه يوم الخامس من شهر مارس وكانت عدد الحالات هى 46 الف حالة تقريبا. اذا اخذنا فى الاعتبار ان النسبة بين الاصابات والحالات فى ايطاليا حسب النموذج هي 40 . اذن تكون حالة الاصابات قد بلغت مليون وثمانمائة واربعين الف اصابة. واذا افترضنا ان معظم هذه الحالات تمر بلا مشاكل وان 0.3% فقط من الحالات تحتاج الى اجهزة تنفس صناعى. نرى ان ايطاليا احتاجت فى تلك الفترة الى 6 الاف جهاز تنفس صناعى واذا علمنا ان ايطاليا تحتوي فقط على 7 الاف سرير طبى مجهز للتعامل مع هذه الحالات. نستطيع ان نستوعب الان صور المرضى وهم يموتون فى ممرات المستشفيات وخنقهم احياء بسب عدم كفاءة اجهزة الدولة الايطالية للتعامل مع تلك الازمة

الطريقة الثالثة هى طريقة مناعة القطيع Herd immunity وقد اشرنا بالاعلى اليها. وهى تستهدف حماية الشريحة الاضعف من المجتمع والحول دون وصول المرض اليهم مع تعريض باقى طوائف المجتمع بشكل مسيطر عليه للمرض. ولم تتبع هذه الطريقة رسميا سوى انجلترا ولكنها كبدتها خسائر باهظة وتخلت عنها بشكل غير رسمى بعد اصابة رئيس وزرائها نفسه بهذا المرض بل وقد كان قاب قوسين او ادنى من الوفاة. وهناك ايضا السويد اللتى تعلن رسميا انها لاتتبع سياسة مناعة القطيع. لكن فعليا فان اجراءات فتح البلاد اللتى تتبعها هى تطبيق عملي لاستراتيجية مناعة القطيع.

والزمن سوف يخبرنا فى النهاية من هو كان الأفضل فى التعامل مع تلك الجائحة