كرة القدم هي أكثر رياضة شعبية فى العالم. والكثيرون فى العالم العربى يتابعون الدوريات المحلية والأوروبية. وسنقوم اليوم بتنظيم مسابقة دوري خاصة بنا ستفاجئ المهتمين منا بكرة القدم بان هناك أشياء يظنونها بديهية وتحصيل حاصل مع أن الامر ليس كذلك. اما لغير المهتمين بكرة القدم فموضوع اليوم يمكننا تطبيقه أيضا فى ميادين اخرى مختلفة تماما. فهذه هى قوة الرياضيات التطبيقية وعلم المعلوماتيات.

للتذكير بمسابقة الدوري فهى مسابقة رياضية تتكون من مرحلتين. تسمى الاولى دور الذهاب والثانية دور الأياب. وفى دور الذهاب يلعب كل أسبوع كل فريق ضد أحد الفرق الأخرى اما على ملعبه أو على ملعب الفريق المنافس. وينتهى دور الذهاب عندما يقابل كل فريق باقي الفرق المنافسة. ويجرى دور الأياب على نفس الوتيرة وبنفس الترتيب فقط يتغير الملعب. فاذا كانت مقابلة دور الذهاب تمت على ملعب الفريق أ فان مقابلة دور الأياب تتم على ملعب الفريق ب.

ودعونا نبدأ بتحديد العدد المثالي للفرق المشاركة فى الدوري الخاص بنا. فمن السهولة ان نرى ان عدد الفرق ينبغى ان يكون عددا زوجيا. لانه لو كان عددا فرديا فسيبقى كل أسبوع فريق بدون منافس يمكنه ان يقابله. وفي الدوريات الاوروبية الكبيرة نجد أن عدد الفرق يكون 18 أو 20 . لكن هذا الرقم كبير لعرض فكرة اليوم بشكل مبسط. فدعونا نختار عددا زوجيا صغيرا. ولكن على الجانب الأخر فأعداد مثل 2 و 4 هى أعدادأصغر من اللازم فدعونا نفترض اننا نريد ان ننظم مسابقة دوري لستة فرق رياضية!!

فلنبدأ بتنظيم دور الذهاب. ودعونا نحدد عدد الأسابيع اللازمة للانتهاء منه. فحيث أن هناك ستة فرق وكل فريق ينبغى ان يقابل فى كل أسبوع احد الفرق الخمسة الأخرى فاننا سنحتاج الى خمسة أسابيع. أليس كذلك؟ هذا ايضا ما نعهده فى الدوريات الاوروبية اللتى تتكون من 20 فريقا فهي تحتاج الى 19 أسبوع لعب من أجل اتمام دور الذهاب ومثلهم لأتمام دور الأياب. اذن دعونا نعد جدول دور الذهاب. وهذا الامر يبدو سهلا. بل دعونا نكون متساهلين فنسمح فى جو من الروح الرياضية للمتنافسين أن يختاروا أنفسهم. ولنفترض ان الأسابيع الثلاثة الاولى جرى فيها الأمر على الصورة التالية:

ألأسبوع الأول: الفريق 1 ضد الفريق 2 و الفريق 3 ضد الفريق 5 والفريق 4 ضد الفريق 6
الأسبوع الثاني: الفريق 1 ضد الفريق 3 و الفريق 2 ضد الفريق 6  والفريق 4 ضد الفريق 5
الأسبوع الثالث:الفريق 1 ضد الفريق 4 و الفريق 2 ضد الفريق 5  والفريق 3 ضد الفريق6

اذن بعد ان نجحنا فى تنظيم الأسابيع الثلاثة الأولى بمنتهى السهولة واليسر دعونا نوجه أهتمامنا نحو الأسبوعين الأخيرين: الرابع والخامس. لكننا هنا سنواجه مفاجأة غير سارة. لماذا؟ نري أن الفرق 1 و 5 و 6 لم تقابل بعضها نهائيا حتى الأن. فمازال أمام الفريق 1 مباراتان امام الفريقين 5 و 6 . وكذلك بالنسبة للفريق 6 فعليه ان يقابل 5 و 1 وكذلك 5 عليه ان يقابل 1 و6 . لكن اي الفرق بأمكانها ان تلعب فى الأسبوع الرابع؟ اذا افترضنا مثلا ان الفريق الأول سوف يقابل الفريق الخامس فلن يجد الفريق السادس منافسا يقابله فى الأسبوع الرابع لأن خصميه الوحيدين المتبقيين مشغولان باللعب امام بعضهما. وكذلك الحال عند عمل أى أختيار اخر فسوف يستطيع فريقان اللعب بينما يبقى الفريق الثالث منتظرا! ولحل هذه المعضلة  فاما ان يلعب الفريق 1 أو 5 فى الأسبوع الرابع مباراة ثانية ضد الفريق 6 لكن هذا يخالف قوانين المسابقة بأن يلعب كل فريق مباراة واحدة فى الأسبوع. أو ان نمد المسابقة أسبوعا سادسا تقام فيه المباراة بين الفريق 6 واحد الفريقين 1 أو 5 . لكن هذا مرة اخرى يخالف الهدف اللذي وضعناه لانفسنا بانهاء دور الذهاب فى خمسة اسابيع فقط. وتتكرر نفس المشكلة بين الفرق 2 و 3 و 4 حيث انها أيضا لم تقابل بعضها نهائيا حتى الأن. وفي النهاية سنجد انفسنا عرضة لسخرية الأخرين حيث اننا عجزنا عن تنظيم شئ يبدو هينا وهو تنظيم مسابقة تضم 6 فرق.

دعونا الأن نري خوارزمية تستطيع ان تنظم ذلك الأمر لنحصل على النتيجة اللتى نصبو اليها. وهذه الخوارزمية جميلة جدا. اولا فهي بسيطة والأفكار البسيطة دائما جميلة. والأمر الثانى انه تتقاطع عندها ميادين رياضية مختلفة مما يعطيها عمقا اضافيا ويزيدها جمالا. اما هذه الميادين الرياضية فهى ميدان المعلوماتيات وميدان الهندسة الأقليدية بشقيها المستوية والفراغية.

أما ميدان المعلوماتيات Informatics ويوجد له أسم اخرولكنه غير مناسب البتة وهو علم الكمبيوتر computer science.  فهذا الميدان ليس له علاقة بالكمبيوتر من قريب أو بعيد. والكلمة اصلها ألماني Informatik وهى كلمة مركبة من جزئين وهما Information بمعنى معلومات و Mathematik بمعنى الرياضيات. فتعنى الكلمة رياضيات المعلومات. وهي من هذا المنطلق تعتبر أحد أفرع الرياضيات التطبيقية. ومن التقنيات الهامة فى هذا الميدان تقينة الرسم Graph حيث نعبر عن المشكلة اللتى نتعامل معها كرسم فنرسم العناصر الأساسية لمشكلتنا فى صورة دوائر أو نقط أو أى شكل هندسى أخر ونطلق عليها العقد جمع عقدة node. والعلاقات بين هذه العناصر تعبر عنها خطوط تصل بينها. وفي موضوع اليوم فان لدينا 6 عقد تعبر عن الستة فرق. وكل خط يصل بين فريقين يعبر عن مباراة أو مقابلة تتم بين هذين الفريقين.

رسم بياني

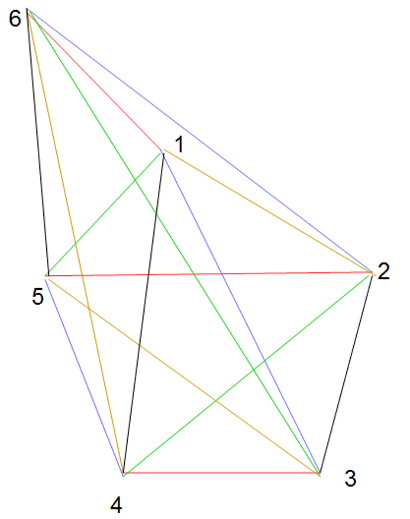
دعونا الان ندخل وسيلة مساعدة اضافية ليست موجود فى التقنية الأصلية وهى الألوان. فالخطوط المرسومة بلون واحد تعبر عن المباريات المقامة فى نفس الأسبوع. ومن الرسم التالي نستطيع ان نرى تنظيما لمباريات الدوري الخاص بنا:

ألاسبوع الأول: الفريق 1 ضد 6 والفريق 2 ضد 5 والفريق 3 ضد 4
الأسبوع الثاني: الفريق 1 ضد 3 والفريق 2 ضد 6 والفريق 4 ضد 5
الأسبوع الثالث: الفريق 1 ضد 5 والفريق 2 ضد 4 والفريق 3 ضد 6
الأسبوع الرابع: الفريق 1 ضد 2 والفريق 3 ضد 5 والفريق 4 ضد 6
الأسبوع الخامس:  الفريق 1 ضد 4 و الفريق 2 ضد 3 والفريق 5 ضد 6

وعندما نتأمل الرسم سنرى هرما واذا تاملنا الخطوط اللتى تعبر عن مباريات الاسبوع الأول سنجد خطوطا باللون الأحمر لا تتقاطع فالخطان 2-5 و 3-4هما خطان متوازيان اما الخط 1-6 فهو خط متخالف فراغيا لكليهما. ونذكر بأنه اذا تقاطع خطان لهما نفس اللون فى عقدة فان هذا يعنى ان هناك فريقا يشارك فى مبارتين فى نفس الأسبوع. اما اذا لم تتقاطع الخطوط نهائيا مهما مددناها فان هذا يعنى ان مشاركة فريقين فى مبارتين فى أسبوع واحد هو امر مستحيل

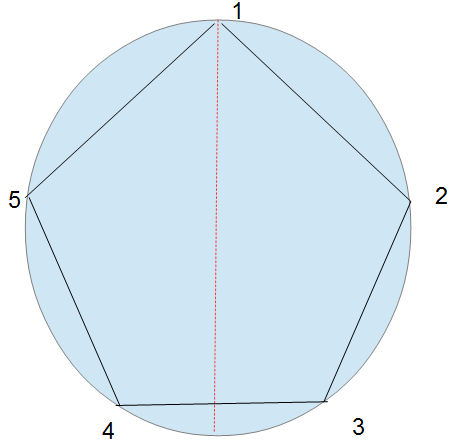
اذن خطتنا هى أن ننشئ شكلا فراغيا وهو الهرم ووننشئ فيه خطوطا فراغية لا تتلاقى. ولأجل ذلك نقوم بالخطوتين التجهيزيتين التاليتين:
1 نأخذ النقطة الأخيرة ونجعل منها رأس الهرم
2 نوزع النقاط المتبقية على محيط دائرة بشكل منتظم. ففى المثال الحالى نحصل على خماسى مننتظم. واذا كان عندنا ثمانية فرق فسنحصل على سباعى منتظم فى القاعدة. واذا كان عدد الفرق الكلى هو مائة فسنحصل فى القاعدة على شكل منتظم يتكون من تسعة وتسعين ضلعا. ونلاحظ انه فى جميع الاحوال يكون عدد نقاط القاعدة فرديا.

اما الخوارزمية نفسها فهى تتكون من الخطوات الثلاثة التالية:
1 فى كل أسبوع نصل رأس الهرم باحد نقاط القاعدة. ويعبر هذا الخط عن أحد مباريات ذلك الأسبوع
2 الخطوة الثانية هى خطوة مساعدة وهى خطوة ذهنية ولا يشترط اجراؤها فعلا. لكن من المفضل ان نفعلها لانها ستساعدنا فى تبسيط فكرة الحل. هنا نصل نقطة القاعدة السابقة مع مركز الدائرة لنحصل على قطر يقسم الدائرة والشكل المنتظم فى القاعدة الى نصفين متطابقين متماثلين. ويمكننا ان نعتبر هذا القطر وكأنه مرأة عاكسة. وعلينا ان نجعل هذا القطر يأخذ اتجاها جنوبيا شماليا. فأن لم يكن كذلك فعلينا ان ندير الهرم فى عكس اتجاه دوران عقارب الساعة حتى يأخذ ذلك القطر دائما اتجاها جنوبيا شماليا
3 تكون النقاط الباقية موزعة على يمين ويسار القطر فى صورة منتظمة. ثم نصل كل نقطة علي يمين القطر بصورتها على يساره وكل خط نصله يعبر عن مقابلة فى هذا الاسبوع.

دعونا نناقش برهان ما فعلناه توا. فحيث ان عدد النقاط الكلية هو عدد زوجى ونحن نقوم كل أسبوع باستبعاد نقطتين: نقطة ثابتة وهى رأس الهرم ونقطة متغيرة كل أسبوع وهى النقطة اللتى نرسم منها القطر. اذن يتبقى لدينا دائما عددا زوجيا من النقاط. وبما أن قاعدة الهرم هى شكل منتظم وبما أن القطر المذكور يقسم الزاوية عند النقطة المختارة الى نصفين متساويين فانه يقسم الشكل باكمله الى نصفين متطابقين متناظرين متماثلين. ويكون القطر فى هذه الحالة محورا للتماثل. ويكون الخط الواصل بين النقاط المتبقية وانعاكساتها عموديا على محور التماثل. اذن فهى خطوط متوازية وعدد هذه الخطوط هو (n-2)/2 أو n/2-1 ومن السهل ان نرى ان الخط الواصل بين رأس الهرم والنقطة على رأس محور التماثل تصنع خطا فراغيا مخالفا للخطوط المتوازية السابقة لانها لو قطعها لكان يقع معها فى مستوى واحد ويكون معنى ذلك ان رأس الهرم يقع بداخل قاعدته وهذا يخالف مفهوم الهرم. اذن نحصل دوما باستخدام هذه الطريقة على n/2 من الخطوط اللتى لا تتلاقى ابدا وذلك لكل أسبوع.

وبما اننا نغير محور التماثل فنحصل على مقابلات جديدة كل أسبوع. فمثلا نحن فى الاسبوع الأول عندما يكون رأس المحور النقطة 1 فاننا نصل جار النقطة 1 الأول من جهة اليمين بجارها الاول من جهة اليسار فنصل 2 ب 5 ثم نصل جار النقطة 1 الثانى من جهة اليمين بجارها الثانى من جهة اليسار فنصل النقطة 3 ب4 . وفى الأسبوع الثانى نكون نتعامل مع جيران النقطة 2 من جهتى اليمين واليسار. وحيث ان النقطة 2 تختلف عن النقطة 1 مكانيا فلذلك يختلف ايضا جيرانهما ونحصل على مباريات جديدة كل أسبوع. وهذه الخوارزمية تنجح دائما سواء كان عندنا ستة فرق او مئين او مليون.

دعونا الأن نناقش مشكلة اخري. فحيث ان كل فريق يلعب نصف مبارياته على ملعبه والنصف الأخر على ملاعب الفرق المنافسة الأخري فاننا بكل تأكيد لانريد تنظيما للدوري يجعل فريقا ما يلعب كل مباريات دور الذهاب على ملعبه ثم يلعب مباريات دور الأياب على الملاعب الأخرى. فهذا التنظيم سيئ ويخل بمبدأ تكافؤ الفرص بين الفرق المختلفة. ان ما نصبو اليه هو ان يتم التناوب فى تغيير الملعب. بحيث يلعب الفريق هذا الاسبوع بداخل ملعبه ثم الأسبوع المقبل فى خارج ملعبه وهكذا دواليك. لكن هل هذا الامر ممكن تحقيقه عمليا بنسبة 100%؟ دعونا نناقش هذا الامر رياضيا!

دعونا نرمز للمباراة اللتى تقام داخليا بالحرف د بينما المباراة اللتى تقام خارجيا بالحرف خ. فاذا بقينا فى اطار المثال ذي الستة فرق السابق فسنطلق على الفرق “دخدخد” اذا كانت اول مباراة مقامة لها فى الداخل او “خدخدخ” اذا كانت اول مباراة لها مقامة فى الخارج ثم تتناوب تغيير الملعب بعد ذلك باستمرار. وفي حين اننا نرى انه من السهل ان يوجد فريق نصف بمباراته ب “دخدخد” لكن هل يمكن ان يوجد فريقان ينطبق عليهما معا تلك الخاصية؟ ألأجابة هي أن ذلك مستحيل! فمتى وكيف يلتقى اذن هذا الفريقان مع بعضهما؟ ففى الأسابيع الفردية ينبغى ان يبقى الفريقان بداخل ملعبهما بينما فى الاسابيع الزوجيه عليهما ان يغادراه. ونفس الأمر ينطبق عل سلسلة اللعب “خدخدخ”. اذن من المستحيل رياضيا ان يتناوب أكثر من فريقين لعب مباراتهم بداخل ملعبهم وخارجه. وان كان هذا ممكن بالنسبة لفريقين فقط!

دعونا اذن نغير فى اشتراطاتنا فنحن نريد الأن ان يتناوب فريقان فقط لعب مبارياتهما داخل ملعبهما وخارجه بنسبة 100%. اما بالنسبة لباقى الفرق فعليهم ان يتناوبوا مباراياتهم داخل ملاعبهم وخارجها مع السماح لهم بكسر ذلك التناوب مرة واحدة فى الدور الواحد. فهل هذا ممكن؟ الاجابة هى نعم بل وممكن تحقيقه بنفس الخوارزمية السابقة لكن بعد عمل بعض التعديلات البسيطة.

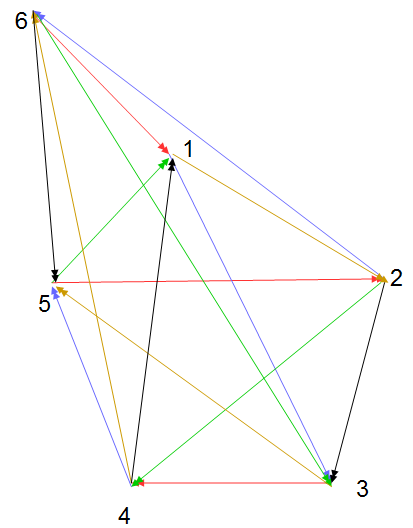
فهنا يجب ان ندخل وسيلة مساعدة اخري وهى الأسهم. فعندما نرسم سهما من النقطة 6 الى 1 فمعنى ذلك ان الفريق 6 يذهب الى الفريق 1. أو أن المباراة داخلية بالنسبة للفريق 1 وخارجية بالنسبة للفريق 6. ثم دعونا نزيد على الخوارزمية السابقة النقطتين التاليتين:

1 عندما نصل رأس الهرم باحدى نقاط القاعدة تكون المباراة داخلية بالنسبة لرأس الهرم عندما يكون الرقم عند القاعدة زوجيا والعكس صحيح
2 عندما نصل الخطوط فى قاعدة الهرم نطبق القاعدة التالية: النقاط الواقعة على يمين محور التماثل ويكون موقعها -لاحظوا موقعها وليس قيمتها – من الأعلى الى الأسفل فرديا تكون المباراة بالنسبة لها داخلية. بينما المواقع الزوجية تكون المباراة بالنسبة لها خارجية.

دعونا نرى ذلك بالتفصيل فى ضوء المثال السابق: فى الأسبوع الأول يكون الخط الواصل بين رأس الهرم 6 والنقطة 1  وبما أن 1 هو عدد فردي فتكون المباراة فى ملعب الفريق 1. أما بالنسبة للمحور المار بالنقطة 1 فتقع النقاط 2 و3 على يمينه بينما تقع النقاط 4 و5 على يساره. وتحديدا فأن النقطة 2 هي الاولى من أعلى والنقطة 3 هى الثانية من أعلى. اذن يكون الفريق 2 هو صاحب الملعب ضد الفريق 5. بينما يكون الفريق 4 هو صاحب الملعب فى المباراة بين الفريقين 3 و 4

أما فى الأسبوع الثاني فيكون الخط الواصل بين رأس الهرم والنقطة 2 وبما ان 2 هو عد زوجي.فتكون المباراة فى ملعب الفريق 6. ثم بالنسبة للمحور المار بالنقطة 2  تقع النقط 3و4 على يمين المحور بينما تقع النقط 5 و1 على يساره. وتحديدا فأن النقطة 3 هي الاولى من أعلى ثم النقطة 4 هى الثانية من أعلى. فيكون الفريق 3 هو صاحب الملعب فى مقابلته ضد الفريق 1. بينما يكون الفريق 5 هو صاحب الملعب فى المباراة بين الفريقين 5 و4

ويكون جدول المباريات كالتالي مع مراعاة اننا نكتب الفريق صاحب الملعب اولا
الاسبوع الاول: 1 ضد 6 و 2 ضد 5 و 4 ضد 3
الأسبوع الثاني: 3 ضد 1 و 6 ضد 2 و 5 ضد 4
الأسبوع الثالث: 1 ضد 5 و 4 ضد 2 و 3 ضد 6
الأسبوع الرابع: 2 ضد1 و 5 ضد 3 و 6 ضد 4
الأسبوع الخامس. 1 ضد 4 و 3 ضد 2 و 5 ضد 6

ونرى مما سبق ان الفريقين 1 و 6 يتناوبان تغيير الملعب بشكل مطلق. بينما باقى الفرق الاخرى تفعل ذلك باستثناء وحيد. ودعونا الأن نقترب من الواقع أكثر ونعطى الفرق السابقة اسماء ولانتعامل معها كأنها ارقام مجردة. فلنفرض ان الفرق الستة اسماؤها كالتالي:
1 برشلونة
2 ريال مدريد
3 بايرن ميونيخ
4 بروسيا دورتموند
5 ارسنال
6 يوفنتوس

اذن فاي الفرق يمكنها ان تكون الفريق رقم 1؟ دعونا نجري قرعة وستكون لدينا 6 أحتمالات. ثم بعد تحديد الفريق الأول سيتبقى لدينا 5 أحتمالات لتحديد أسم الفريق رقم 2 و4 أحتمالات لتحديد اسم الفريق رقم 3 وهكذا فيكون لدينا فى النهاية حاصل ضرب 6 في 5 في 4 فى 3 في 2 في 1 من الأحتمالات او 720 احتمالا لتوزيع اسماء الفرق على الأرقام الموجودة. اى لو اننا كررنا هذه المسابقة كل سنة فسنستطيع بتغير توزيع الفرق على الأرقام استخدام جدول المباريات السابق لمدة 720 عاما وبدون أن يشعر فريق بتكرار نمظ تنظيم المباريات..

لكن الأمر يجرى فى الواقع بصورة اكثر تعقيدا مما سبق فلقد وضعنا حتى الأن شرطين وهما ان يكون عدد اسابيع لعب دور الذهاب يقل عن عدد الفرق المشاركة بواحد. والشرط الثانى هو ان تتناوب الفرق اللعب بداخل ملعبها وخارجه لأقصى درجة ممكنة. لكن هناك شروط اخرى اضافية تزيد المسألة تعقيدا!

فمثلا قد يكون هناك فريقان من نفس المدينة فلا يمكن أن يلعب الفريقان داخليا فى نفس الأسبوع لأن الأستاد الموجود لن يستوعب ذلك الأمر. او بسبب متطلبات امنية حيث ان تنظيم المباريات فى داخل المدينة يشكل عبئا تنظيميا على كاهل المدينة فلايجب ان نفعل ذلك مرتين فى نفس الأسبوع  الا اذا كان الفريقان يواجهان بعضهما.

وهناك شرط اخر قد يتعلق بالاستاد فقد يكون فى تاريخ معين غير مهيئ لأستقبال مباريات رياضية بسبب أعمال صيانة أو لأنه محجوز لأجل مناسبة أخري. ثم ان هناك أمر اخر. فغالبا يوجد لكل بطولة فريقان ينافسان على الفوز بها. و سيكون أمر سخيف لو تقابل هذان الفريقان فى بداية البطولة ومن الافضل تأخير المقابلة بينهما. بل انه قد توجد مقابلات بين فرق معينة تأخد دائما طابعا مثيرا لاسباب مختلفة ولأجل ذلك فانه من الأفضل توزيع تلك المباريات المثيرة والشيقة على مدار العام ولاتكون كلها مركزة فى فترة زمنية قصيرة.

فماذا اذن اذا كان عندنا 18 فريق وأردنا مراعاة الأمور السابقة كلها؟ قد نرى مثلا أننا بعد تنظيم جدول المباريات وفقا للخوارزمية السابقة نستطيع ان نقوم بعمليات تباديل وتوافيق لنحصل على جدول مباريات جديد نستطيع تقييمه كل مرة حتى نحصل على افضل تنظيم لمباريات الدوري. لكن هنا دعونى اذكركم بما تحدثنا عنه في موضوع سابق بان بديهة الأنسان غير مهيئة للتعامل مع العمليات الاحصائية ولا تستوعبها تماما. فالأحتمالات الممكنة فى هذه الحالة كما أوضحنا فى المثال السابق هى مضروب 18 أو حاصل ضرب 18 فى 17 فى 16 فى  15 الى اخره حتى نصل الى 1. وهذه قيمة هائلة جدا وتساوي 6400000000000000 -اربعة عشر صفرا-. واذا افترضنا ان لدينا جهاز كمبيوتر يستطيع ان يقوم بمليار عملية تقييم فى الثانية الواحد فأننا سوف نحتاح الى 74 يوما من العمل المتواصل حتى ننتهى الى الأختيارالمثالي.

اذن الحصول على تنظيم ما للبطولة عملية ليست صعبة تماما اذا تجنبنا الفخاخ اللتي عرضناها  لكن الوصول الى التنظيم الأمثل هى عملية صعبة جدا ولا تتعجبوا ان علمتم ان هناك أبحاثا علمية متخصصة تتم فى هذا المجال.