يعد فيثاغورث من اهم الفلاسفة اليونانيين. فهو كان معدودا من حكماء الاغريق السبعة اللذين علا نجمهم قبل العصر السقراطى. وبالاضافة الى ذلك فقد كان رياضيا فذا و فيزيائيا مقتدرا وموسيقيا رائدا اكتشف السلم الموسيقي. كما انه كان سياسيا مخضرما خاض معارك سياسية مثيرة بل انه قام بكتابة دستورا لليونانيين القاطنين في ايطاليا. وبالاضافة لذلك فقد اسس مدرسة علمية كانت الاشهر و الاحسن في زمانها.
مع ذلك تبقى جوانب كثيرة فى حياة فيثاغورث والفيثاغورثيين غير معروفة ولكنها مؤثرة. صحيح انها اقل شهرة ولكنها اكثر اثارة وغرابة. وهذه الجوانب هي موضوع اليوم.
فيثاغورث كان يؤمن بتناسخ الارواح وعلى المستوى الشخصى كان يعتقد بان روح البطل الطروادي اويفروبوس قد حلت فيه. ولذلك فقد كان نباتيا متزمتا. فقد كان يعتقد بان الارواح تسكن حتى اجساد الحيوانات. لكن الامر الغير مفهوم هو تحريمه وكرهه الغريب لخضار معين وهو: اللوبيا. فقد كان يأمر تلاميذه باجتنابها ويقول انها تسبب الانتفاخ و تثير الاشمئزاز لانها تشبه الاعضاء التناسلية. وكان فيثاغورث ينهى اتباعه عن لبس الصوف وينصحهم بان يقربوا زوجاتهم في الشتاء و أن يعتزلوهن في الصيف.
وكان للفيثاغورثيين نوعان من المحاضرات: محاضرات علنية متاحة للجميع الهدف منها تثقيف الشعب وتحبيبه في الرياضيات والعلوم وتقريب المواضيع العلمية للناس. والنوع الثانى من المحاضرات كانت محاضرات سرية لا يحضرها سوي تلاميذ مدرسة فيثاغورث وكلهم قد اقسموا الا يبوحوا ابدا بمضمون تلك المحاضرات ويجب ان يبقوها سرا في طى الكتمان.
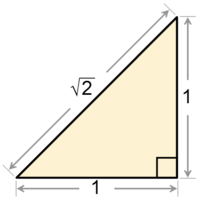
وموضوع اليوم يتعلق باحد هذه المواضيع السرية وهو خاص بالاعداد الغير نسبية. وللتذكرة فقد رفض الفيثاغورثيون الاعداد الغير نسبية واطلقوا عليها اسم الاعداد البلهاء او الاعداد الغير منطقية وهذا هو الترجمة الحرفية لكلمة irrational numbers . وقالوا ان هذه الاعداد غير موجودة في الكون البتة. ولكن المفاجاءة ان اكتشف الفيثاغورثيون ان هذه الاعداد الغير نسبية موجودة في الطبيعة بوفرة رهييبة. بل ولهول المفارقة فان القانون المرتبط اسمه باسم معلمهم اي قانون فيثاغورث ليس الا اداة رهيبة لانتاج تلك الاعداد الغير نسبية. و لتوضيح ذلك يقول قانون فيثاغورث ان مربع وتر الزاوية القائمة يساوي مجموع مربعى ضلعى الزاوية القائمة في المثلث القائم الزاوية. فالأن اذا تخيلنا ان هناك مثلثا قائم الزاوية طولا ضلعى زاويته القائمة 1 متر اذن فسيكون مربع الوتر يساوي مربع العدد واحد وهو طول الضلع الاول زائد مربع العدد واحد وهو طول الضلع الثانى. فيساوى مربع الوتر في النهاية 2. ومن هنا يكون طول الوتر نفسه جذر 2. الى هنا لا توجد اى مشكلة. لكن كيف يمكننا ان نعبر عن العدد جذر 2 في صورة عدد نسبي؟ هل نعبر عنه مثلا في صورة العدد 7/5 ؟ في الحقيقة هذه القيمة تقريب جيد وتساوى 1.4 ولكنه غير كافى تماما حيث ان مربع 1.4 يساوي 1.96 . اى ان قيمة جذر 2 اكبر من ذلك.
دعونا الان نفكر كما كان الاغريق يفكرون: لو اننا تخيلنا مسطرة صغيرة او قضيب قياس طوله يساوي 20 سم او خمس متر فانه سوف ينطبق 5 مرات تماما على كلا من ضلعى الزاوية القائمة السابق ذكرهما . ولكنه في المقابل سوف ينطبق 7 مرات على الوتر وسيبقى جزء متبقى طوله اقل من 20 سم فلا يمكننا ان نغطيه بقضيب القياس بالكامل مرة اخرى. اذن فانه فلا يمكننا تطبيق قضيب القياس على الوتر عدد صحيح من المرات.
توقع الاغريق انه لابد وان يوجد قضيب قياس اخر ذو طول مختلف مثلا 10 سم او 13سم او اي طول اخر بحيث ينطبق عدد صحيح من المرات على كل من ضلعى الزاوية القائمة ووترها. ولكن المفاجاءة كانت تكمن في ان الفيثاغورثيين قد اكتشفوا ان قضيب قياس كهذا غير موجود ولا يمكن ان يكون موجودا ابدا وحصلوا على برهان رياضى لهذا. وللمهتمين بمعرفة برهان لماذا جذر 2 عدد غير نسبى يمكنهم مرجعة ذلك الرابط.
ولان هذه النقطة في غاية الاهمية دعونا نستفيض فيها قليلا: اذا تخيلنا ان لدينا خطا طوله 3 متر وان لدينا قضيب قياس طوله 1 متر. فقضيب القياس سوف ينطبق على هذا الخط 3 مرات تماما وبامكاننا ان نقيس ذلك الخط بكل دقة. ماذا الان لو كان طول الخط هو 1.25 متر؟ بالطبع قضيب القياس السابق لن يفى بالغرض لانه لن ينطبق عدد صحيح من المرات على الخط ولكننا باستخدام قضيب قياس اخر اقصر طوله مثلا 25 سم فسوف نستطيع قياس الخط السابق. فسوف ينطبق 5 مرات تماما. اذا ماذا لو كان طول الخط 17 سم؟ مرة اخري قضيب القياس السابق لن يفى بالغرض لكن ربما قضيب قياس طوله 1 سم فسوف يستطيع ذلك. وهكذا فمن حيث المبدأ لقياس اى طول ما فما علينا الا اختيار قضيب قياس ذو طول قصير امتر او اسم او امم لايهم فلابد وان ينطبق في النهاية على الخط المطلوب قياسه عدد صحيح من المرات. لكن المفاجأءة ان اكتشف الفيثاغورثيون ان خط طوله جذر 2 متر لن يستطيعوا ان يجدوا اى قضيب قياس ذي ايى طول لكى ينطبق على هذا الخط عدد صحيح من المرات. فحتى لو كان طول هذا القضيب اقل من قطر ذرة فلن ينطبق على المسافة المذكورة عدد صحيح من المرات. وكان هذا التصور بالنسبة للفيثاغورثيين امرا مجنونا ولذلك اطلقوا على هذه الاعداد الاعداد الغير منطقية وانكروا وجودها.
اذن فالمصيبة اللتى حلت بالفيثاغورثيين انهم ادركوا بما لا يدع مجالا للشك ان جذر 2 عدد غير نسبى. وبينما هم يبحثون عن مخرج لهذه الورطة اللتى تعصف بفلسفتهم بالكامل لم يستطع احد التلاميذ كتمان السر وهو هيباسوس وهو الرياضى المقصود في العنوان فافشى هذا السر في المدينة وصارت فضيحة الفيثاغورثيين مشهورة وعرف بامر ورطتهم كل انسان.
وتمت عقد محاكمة سريعة ليهباسوس من قبل زملاؤه واخوانه في مدرسة فيثاغورث ولم يجدوا سوى عقوبة واحدة له: وهى الاعدام. واختلفت الروايات في طريقة تنفيذ حكم الاعدام. فبعض الروايات تقول بانه تم حمله في قارب وسط البحر ثم القاؤه هناك ليموت غرقا. ورواية اخري تقول بانه تم اعدامه عند الشاطئ عن طريق اجباره بان يتجرع كأس سم. ورواية ثالثة تقول بانه تم حبسه في مكان لا يصل اليه بشر حتى مات هناك.
اما فيثاغورث نفسه فقد لقى هو ايضا حتفه بطريقة غريبة. و لم يكن السبب في قتله الاعداد النسبية او الصفر بل شئ عجيب اخر. ونهاية فيثاغورث تشبه نهاية المتنبى الى حد كبير. فالمتنبى كان له خصوم كثيرون يتمنون قتله فقد كان هجاءا هاجم الكثيرين في شعره وجعلهم موضع تندر. وفي احد المرات تربص به خصومه لقتله ولكن المتنبى نجح في الفرار وهرب. وهنا قال له خادمه اللئيم : اتهرب يا سيدي؟! . الست انت القائل
الخيل والليل والبيداء تعرفنى
والسف والرمح والقرطاس والقلم
فشعر المتنبى بالحرج وعاد بعد ان كان قد نجى وقاتل فلقى مصرعه. ويعرف بيت الشعر هذا باسم البيت اللذي قتل صاحبه!!
اما قصة فيثاغورث تقول بانه كانت هناك جماعة تريد الالتحاق بمدرسة فيثاغورث لكنه سخر منهم ورفض قبولهم وقال لهم انهم غير جديرين بالانضمام الى مدرسته. فشعر هؤلاء بالاهانة والغضب وقرروا الثأر لكرامتهم. فكادوا لفيثاغورث. ففي احد المرات حينما كان فيثاغورث مجتمعا مع تلاميذه في مكان ما حرق الكائدون البيت اللذي يوجد فيه فيثاغورث و تلاميذه وانتظروهم خارج المبنى بالسيوف فمن نجى من الحريق قتلوه بالسيف. وتقول الرواية بان فيثاغورث نجح في الهرب واطلق ساقيه للريح. لكن انتهى به الامر الى حقل لوبيا كان عليه ان يعبره لكي ينجى بحياته تماما. لكن فيثاغورث تذكر مبادئه و انه كان دائما يأمرتلاميذه باجتناب هذا الشئ . وكان عليه ان يقرر هل يخالف مبادئه وينجو بحياته. ام يحافظ عليها ويموت. وتجمد فيثاغورث في مكانه ولم يستطع عبور هذا الحقل فلحق به خصومه فقتلوه!!
وهكذا نري ان الطريق الى ظهور الاعداد الغير نسبية كان وعرا سالت فيه الدماء. لكن بعد ذلك تقبل الاغريق الاعداد الغير نسبية وذكر اقليدس برهان ان جذر 2 عدد غير نسبى وتمت الاشارة الى هذا البرهان اعلى. ولكن الصفر بقى منكرا. فقد كان من السهل انكاره. فبقى مرفوضا حتى حين!!