نتعرف اليوم على قانون المركز الثانى. و للمرة الثانية نتعرف على قانون ينتمى لميدان الهندسة الفراغية. وقد كانت المرة الاولى عندما تعرضنا لقانون المركز الرابع واللذي يفيد بأن عدد الاجسام الافلاطونية هو خمسة. كما ان هذا القانون هو ايضا ثانى مرة نتعرف فيها على قانون منسوب لأويلر حيث كانت المرة الاولى عندما تعرضنا لقانون المركز الخامس الخاص بالعدد ط. ومن قبيل المصادفة الطريفة ايضا ان قانون اليوم يحتوي على العدد 2 في الطرف الثانى من المعادلة. فقانون اليوم يقول ان:
V-E+F=2
حيث ان V هو عدد اركان الجسم الفراغى المحدب وهو مشتق من الكلمة الانجليزية vertex
و E هو عدد حواف الجسم الفراغى المحدب وهو مشتق من الكلمة الانجليزية edge
و F هو عدد اوجه الجسم الفراغى المحدب وهو مشتق من الكلمة الانجليزية face
وفيما يلى نتعرف على القانون بشئ من التفصيل.
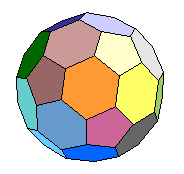
في ميدان الهندسة المستوية من السهل علينا ملاحظة خواص الاشكال المختلفة فالمثلث له 3 اضلاع و 3 زوايا و المربع له 4 اضلاع و اربع زوايا وكذلك الحال بالنسبة الى المخمس فله 5 اضلاع و 5 زوايا الي اخره. ولكن اذا انتقلنا الى ميدان الهندسة الفراغية فان الموضوع لن يكون بهذا الوضوح! نعلم ان الاجسام الفراغية لها عدة سطوح او اوجه. واذا تقاطع وجهان في خط فاننا نطلق على هذا الخط حافة. واذا تقاطعت ثلاثة اسطح على الاقل في نقطة فاننا نطلق على هذه النقطة ركن. اذن الاوجه و الحواف و الاركان هي كلها خواص وسمات واضحة للاجسام الفراغية فهل توجد علاقة بسيطة تربط كل هذه المكونات والصفات الرئيسة ببعضها؟ الاجابة هى نعم. وقانون اليوم يتعامل تحديدا مع هذا السؤال ويقول بانه بالنسبة لاي جسم فراغي محدب سواء كان منتظم ام لا فاننا اذا جمعنا عدد اركان هذا الجسم زائد عدد اوجهه ثم طرحنا من النتيجة عدد حوافه فان النتيجة تكون دائما 2! مثال لهذا المكعب: فالمكعب يحتوي على 8 اركان و 6 اوجه اذن فالمجموع هو 14 فاذا طرحنا عدد حواف المكعب وهو 12 تكون النتيجة 2. و اذا اردنا دراسة اجسام اكثر تعقيدا من المكعب كما الجسم في الرسم فان النتيجة سوف تكون هي نفسها.
اول من توصل الى هذا القانون كان الفيلسوف و الرياضى و الفيزيائي الفرنسي ديكارت René Descartes في القرن السابع عشر. ولكنه لم يستطع ان يبرهن هذا القانون. ثم ذكر ليونيل اويلر هذا القانون في رسالة الى صديقه جولدباخ. ولكنه ذكر انه اكتشف هذا القانون بالنسبة لاي شبكة مسطحة متصلة من الخطوط. وفي الحقيقة فان هناك طريقة معينة نستطيع بواستطها ان نفرد اى جسم فراغى محدب الى شبكة مستوية متصلة بحيث يكون لها نفس عدد الاركان و الاوجه و الحواف. ومن هنا نري ان قانون اويلر للشبكات المتصلة ينطبق ايضا على الاجسام الفراغية المحدبة. و اليوم يوجد اكثر من 19 برهانا منفصلا لهذا القانون.
ومن الرائع ان نتفكر في امر التطور الفكري في ميدان الهندسة او الرياضيات عموما. فالهندسة المستوية لاشك انها بديعة و ساحرة. ولكن عندما ننتقل من الهندسة المستوية الى الهندسة الفراغية فان النقلة لن تكون سهلة. فالانسان يحتاج الى التعامل مع الهندسة الفراغية الى خيال اكثر وقدرة على التخيل اوسع منها في حالة الهندسة المستوية. وقد راينا في قانونين المرتين السابقتين كيف ان الخيال و العقل يتقابلان. ففى قانون الاجسام الافلاطونية الخمسة حسم العقل ان الخيال لن يمكنه ايجاد جسم افلاطوني سادس بينما فتح العقل للخيال الباب في ميدان الاعداد الاولية لتخيل اعداد اولية اكبر و اكبر. لكن في ميدان الهندسة فان هناك مفاجأة فالهندسة ليست مقصورة على 3 ابعاد فقط.بل ان الهندسة تقول ان هناك فضاءات ذوات 4 او 10 او 100 بعد واكثر من ذلك بكثير. لكن كيف يمكن لنا ان نتخيل لنا اجسام تشغل ذلك العدد من الابعاد؟ في الحقيقة اننا لا يمكننا ذلك. فنحن لا يمكننا ان نتخيل اكثر من 3 ابعاد مكانية. اذن حيث يتوقف الخيال ويتعطل تماما فان العقل مازال قادرا على اسقاط احكام قاطعة على هذه الاجسام ذوات الابعاد فوق الثلاثية وبثقة رهيبة !!
ومن هنا نري ان التخيل هو اداة من ادوات العقل يستخدمها حينما يكون استخدامها مفيدا. وحين تبطل هذه الاداة او تعجز فان العقل يستخدم اداة او ادوات اخرى للوصول الى هدفه. وقد تكون هذه الاداة الاخري هي اداة القياس او اداة التجريد حين يبحت العقل بشكل تصوفى حول الحقيقة المجردة خلف الاشياء: ماهو السطح المجرد او مامعنى حافة مجردة او معنى مسافة او خط فعلا؟ والقدرة على التخيل هي نعمة رهيبة يمكن تشبيها بنعمة البصر. ولكن البصر ليست الوسيلة الوحيدة للادراك. لانه لو كان الامر كذلك لما كان من الممكن ان يصبح لطه حسين او لابي العلاء المعري اى شأن.
وفي النهاية نري ان قانون اليوم بسيط وجميل حتى على مستوي صياغته. فاننا نري التناغم في بنائه فنرى ان الحد الاول له اشارة موجبة ثم الحد الثانى في المنتصف له اشارة سالبة ثم الحد الثالث و الاخير له اشارة موجبة مرة اخري.ولسهولة حفظ القانون نلاحظ ان الحد الاول وهوعدد الاركان. والركن هو نقطة اي ان عدد ابعاده صفر. ثم يأتى الحد الثانى اللذي يعبر عن الحواف .و الحواف هي خطوط لها بعد واحد.ثم يأتى الحد الاخير اللذي يعبر عن عدد الاوجه. و الاوجه لها بعدان. لكن جمال القانون ليس مرتبط بشكله وصياغته فقط ولكنه كما نري له معنى عميق ويشى عن روح تصوفية في عالم الهندسة و الاشكال و الاجسام.