فى احد الايام فى نهاية القرن التاسع عشر وعلى مشارف القرن العشرين توجه شاب المانى يافع اسمه ماكس بلانك الى جامعة ميونيخ حيث كان يريد ان يدرس هناك ولكنه كان محتارا فى امره. هل يدرس الفيزياء ام الرياضيات. وفى ذلك اليوم ذهب بلانك لمقابلة استاذ الفيزياء فى الجامعة ليطلب منه النصح والمشورة. فاجابه الاستاذ ان عليه ان يختار الرياضيات. فالفيزياء قد انتهت تماما. وقد اكتشف الفيزيائيون كل شئ و فسروا كل نواحى الحياة تقريبا. صحيح ان هناك امور ثانوية مازالت عالقة لكنها مسالة وقت قريب حتى يتوصل الفزيائيون الى حلها ويغلقون ملف الفيزياء برمته!!
هذا الكلام عندما نسمه اليوم نجده طريفا. فتحديدا بعد هذا الحوار بين الاستاذ والفتى ماكس بلانك قامت فى ميدان الفيزياء ثورات هائلة لم تترك شيئا مما كان قبلها قائما. وكان ماكس بلانك نفسه هو مفجر احد هذه الثورات. فى الحقيقة فان كلام الاستاذ السابق ينبغى ان يكون درسا لنا. فحينما نظن اننا حققنا كل شئ او نكاد فربما نكون لم نبدأ بعد!!
لكن من ناحية اخرى فان كلام استاذ الفيزياء فيه شئ من الصحة. فالفيزيائيون فى ذلك الزمان كانوا قد حققوا نجاحات هائلة فى ميادين مختلفة. يهمنها منها اليوم ميدانان. الميدان الاول هو ميدان الحرارة. حيث توصل علم الميكانيكا الاحصائية الى ان ظاهرة الحرارة ليست الا طاقة الحركة لجزيئات المادة. فاى مادة ما تتكون من جزيئات دائمة الحركة. اى ان لها طاقة حركة. وتظهر لنا طاقة الحركة هذه فى صورة حرارة. وتوصل الفزيائى ستيفان بولتزمان الى قانون هام جدا يربط بين طاقة اهتزاز جزئ ما ودرجة حرارته المطلقة او:
E(vibration)=K*T 1
حيث T درجة الحرارة المطقق و K هو ثابت فيزيائى يعرف بثات بولتزمان . اما E فهى الطاقة الاهتزازية وتساوي مجموع طاقتى الحركة والوضع.
لكن من ناحية اخرى مما تتكون الجزيئات؟ انها تتكون من ذرات اللتى بدورها تتكون ممن جسيمات مشحونة وبخاصة الالكترونات. وهنا نصل الى الميدان الثانى وهو ميدان الديناميكا الالكترونية. حيث قال ماكسويل ان اى جسيم مشحون يتسارع تصدر عنه موجات كهرومغناطيسية. واذا ربطنا هذا الكلام بالفقرة السابقة. نصل الى ان اي جسم في هذا الكون له حرارة اى تهتز جزيئاته. اى تتسارع شحناته. اي لا بد وان تصدر عنه موجات كهرومغناطيسية.
وكان هذا فى حقيقة الامر انجاز جديد يضاف الى انجازات الفيزياء فهو يربط ميدان الحرارة بميدان الموجات الكهرمغناطيسية. كما ان التجربة والواقع يؤكدان ذلك تماما. فالحرارة تتولد عنها موجات كهرمغناطيسية واشهر هذه الموجات هي تلك اللتى نستطيع ان نراها. او الضوء المنظور. فاذا سخنا قطعة من الحديد الي درجة عالية فانها تتوهج بلون احمر. واذا رفعنا درجتها فانها تتوهج بلون اصفر واذا رفعنا درجة حرارتها اكثر فاننها تتوهج بلون ابيض. ونفس النتيجة نحصل عليها تماما اذا سخنا قطعة من الفحم بدلا من قطعة الحديد. فاللون اللذي نحصل عليه لا يتوقف على الطبيعة الكيميائية للمادة المستخدمة. ولكنه يتوقف فقط على درجة الحرارة. فلكل درجة حرارة لون معين يعبر عنها.
ونحن نستغل هذه الظاهرة فى تحديد درجة حرارة اسطح النجوم اللتى تبعد عنا بعشرات السنين الضوئية. وذلك عن طريق لونها. كما ان جميع الاجسام حتى اجسادنا تشع موجات كهرومغناطيسية. لكن الموجات المنبعثة من اجسادنا تقع فى مجال الاشعة تحت الحمراء. ونحن نستغل ذلك فى صنع مناظير الرؤية الليلية.
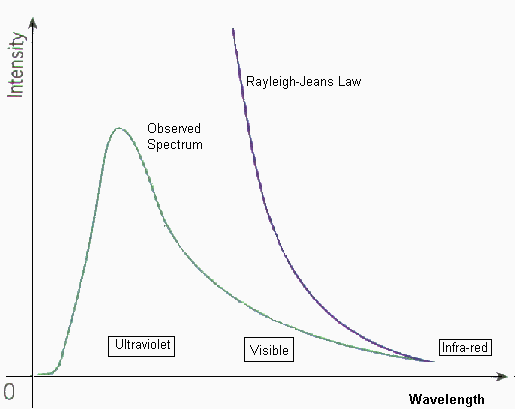
لكن هذا الاحساس الجميل بالنجاح سرعان ما تحول الى احساس مرير بخيبة الامل. صحيح ان قوانين الفيزياء من حيث المبدأ فسرت الرابط بين الحرارة والموجات الكهرومغناطيسية. الا ان فيزيائيي القرن التاسع عشر عندما اتوا الى التفاصيل ووضعوا قوانين الكهربية بجانب قوانين الميكانيكا الاحصائية لم يحصدوا الا خيبة الامل. فالنتيجة اللتى حصلوا عليها رياضيا والمعبر عنها فى الرسم توضح توزيعا للطيف يختلف عنه فى الحقيقة . فالشكل الحقيقى هو الشكل اللذي يبدو منزاحا الى جهة اليسار وله شكل الجرس. اما توزيع الطيف الحسابي فهو مقبول الى حد ما فى الاطياف ذات الطول الموجى العالى. اما الاطياف ذات الطول الموجى القصير فالنتيجة خاطئة تماما. فالحسابات تشير الى ان الاجسام المختلفة تشع اطيافا ذات طول موجى قصير بتركيز عال. بل انها تشع موجات ذات طول موجى يساوى صفر بكثافة لانهائية!
اذن معنى ذلك ان الاجسام فى درجة حرارة الغرفة تبعث اشعاعات حمراء وخضراء وزرقاء الى اخره. اى ان معنى ذلك انه لا يوجد ظلام ابدا حتى فى المساء. فالاضواء المنبعثة من الاجسام المختلفة ومن الهواء تعمى الابصار. بل الادهى من ذلك ان كل الاجسام تشع اشعاعات فوق بنفسجية واشعة رونتجن وجاما وهذه كلها اشعاعات مسرطنة. بل اكثر من ذلك هى اشعاعات قاتلة فورا. ولو كان ذلك صحيحا لم كانت هناك نباتات ولا حيوانات ولا كنا نحن هنا نقرأ هذه السطور. واطلق العلماء على هذه المعضلة تعبير الكارثة الفوق البنفسجية كناية عن الاشعاعات الضارة اللتى تنبعث من كل الاجسام حتى الباردة جدا.
وكانت هذه نهاية عجيية جدا. فبدمج انجح قانونين فى الفيزياء نتجت نتائج مستحيلة. وكأنهم زوجوا اجمل شاب فى قريته باجمل فتاة فى قريتها فانجبا مسخا مخيفا وشيطانا رجيما. على الرغم من ان كل المقدمات كانت تنبئ بعكس ذلك! وعلى عكس كلام استاذ الفيزياء فى بداية الموضوع لم يستغرق هذا الامر وقتا يسير حتى يتم حله. بل دام لسنوات وظل الفيزيائيون عاجزين عن تفسير هذا التناقض حتى اتى ماكس بلانك بنظرية جديدة وحل هذه المعضلة.
لكن حل بلانك كان عالى الكلفة. فهو قال باشياء تبدو مجنونة و غير مقبولة. ولذلك رفض معظم الفيزيائيين حل بلانك رغم ان نتائجه كانت تتطابق الواقع بدقة مذهلة. و الغريب فعلا فى الامر هو رأى بلانك نفسه فى حله. فهو يقول ان مافعله كان عملا يائسا. فهو لم ير سبيل اخر للخروج من مأزق الفيزياء سوى عن طريق هذا الحل. ويقول ان فكرة حله راودته منذ فترة لكنه احجم عن نشرها لعله يصل الى حل افضل. ولكنه لما رأى ان الوقت يمضى ولا هو ولا غيره استطاع ان يحل هذه المشكلة فقرر طرح فكرته لكسر حالة الجمود. و الغريب انه كان يرى فكرته ليست حلا صحيحا نهائيا ولكنه يراها حلا مؤقتا حتى تمضى الفيزياء الى الامام ولكسب الوقت وحتى يظهر فى المستقبل فيزيائى اخر يستطيع ان يحل المعضلة بشكل صحيح. لكن الزمن مضى ولم يأت اخر بحل افضل. بل بقيت فكرة بلانك وقامت عليها نظرية هامة وهى نظرية الكم. لكن ما هى ياترى تلك الافتراضات المجنونة اللتى حل بها بلانك المعضلة واللتى يبدو حتى ان صاحبها يخجل منها؟
فى الحقيقة فان بلانك اتى بافتراضين غريبين. لم يقل بهما فيزيائى قبله. الافتراض الاول ان طاقة طيف كهرومغناطيسى تعتمد على تردد باعثه. هذا الكلام قد يبدو فى اول الامر عاديا لكن لماذا استهجنه واستغربه الجميع. ولماذا لو انه قال انسان بهذا الكلام فى الظروف العادية لكان هذا دليل على جهله فى الفيزياء. ناهيك على ان يصدر هذا الكلام من دكتور فى الفيزياء كبلانك؟
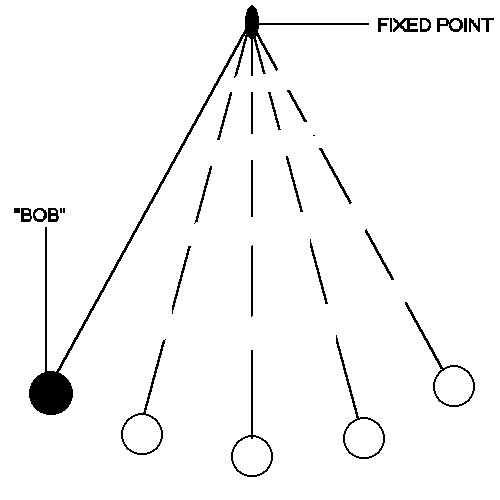
دعونا نرى الامر فى ضوء الفيزياء الكلاسيكية. ودعونا نرى حركة البندول البسيط فهى ايضا حركة اهتزازية. وقد درسها جاليليو واكتشف قانونا هاما عندما كان يستمع الى عظة الاحد فى الكنيسة وكانت العظة مملة وكانت هناك رياح خفيفة تجعل الثرايا فى سقف الكنيسة تتأرجح فلا حظ ان زمن دورة واحد لتأرجح الثريا هو دائما زمن ثابت بغض النظر عن طول التأرجح!
فى حركة البندول البسيط نعلم كلنا ان طاقة النظام الكلية تكون ثابتة لاتتغير خلال التأرجح. واعنى هنا الطاقة الميكانيكية. ففى البداية يكون البندول مستقرا فى المنتصف ثم عندما اقوم برفعه 5 سم مثلا الى جهة اليسار فانى اكسبه طاقة وضع. ثم اقوم بتركه. فان البندول يتأرجح. وتكون طاقة الوضع فى اقصى اليسار اعلى مايمكن حيث يبلغ البندول اقصى ارتفاع. ولكن طاقة حركته تكون صفرا. فاذا تركناه فانه يكتسب طاقة حركة وتقل طاقة وضعه. حتى اذا بلغ المنتصف فتكون طاقة وضعه اقل ما يمكن بينما تكون طاقة حركته اعلى ما يمكن. ولكن فى جميع اللحظات تكون الطاقة الكلية ثابتة
و الان ماذا لو اوقفنا البندول واعدنا الكرة مرة اخرى. لكننا هذه المرة نرفع البندول فى البداية 10 سم بدلا من 5 سم. ففى اى مرة تكون الطاقة الكلية اعلى؟ لاشك انها المرة الثانية حيث اننا نحتاج الى طاقة اعلى لرفع كتلة 10 سم بدلا من 5 سم. اذن فان طاقة الاهتزازة تعتمد على المطال او على السعة القصوى. لكن ماذا عن التردد؟ نعلم كما سبق من قصة جاليليو ان البندول فى المرتين يصنع الاهتزازة فى نفس الزمن. اي ان التردد ثابت. اذن فطاقة البندول المهتز تعتمد على سعته وليست على تردده. ولكن بلانك يقول العكس. يقول ان فى حالة الموجات الكهرومغناطيسية فان طاقة الباعث تعتمد على تردده وليست على سعته!!
لكن لماذا فعل بلانك هذا؟ هو اراد ان يبين لماذا نحن على قيد الحياة الان ولماذا لاتنبعث الموجاتت ذات الطول الموجى القصير. وهو كان بذلك يستغل خاصية غريب من خواص الصفر! فى الحقيقة فان اغلب المشاكل اللتى تنشأ عن الصفر لا يكون الصفر السبب المباشر فيها. وكما يقول اللبنانيون فان الصفر هو نصف مصيبة. لكن المصيبة الكاملة هى فى المالانهاية. واعلم انك عندما تفتح الباب للصفر فانك عاجلا او اجلا فستجد نفسك وجها لوجه مع المالانهاية فالمالانهاية هى الوجه الاخر للصفر على كرة ريمان. وهناك قانون يربط تردد موجة كهرومغناطيسية بطولها الموجى له الصورة التالية:
f= c/L 2
حيث f هو التردد و c هى سرعة الضوء و L هو الطول الموجى.
ومن هنا نري انه عندما يكون الطول الموجى صفر فيكون التردد مالانهاية. اذن وطبقا لفرضية بلانك الجديدة فتكون الطاقة اللازمة مالانهاية. اذن فهى غير موجودة عمليا! وهنا نري ايضا كيف ان الحساب على طريقة ريمان يكون مفيد احيانا فقسمة عدد بخلاف الصفر على الصفر هى كمية معرفة وتعطى مالانهاية!!
اذن فالفرض الاول لبلانك يوضح لنا لماذا لانحصل على الاطياف ذات الطول الموجى القصير. لانها ذات تردد عالي وطاقة هائلة. اذن فالمتبقى على بلانك ان يعطى قانونه الجديد شكل الجرس لتوزيع الطيف كما بينته التجربة العملية. وهنا تأتى الفرضية الثانية لبلانك وهى اشد جنونا من الفرضية الاولى
يقول بلانك ان الباعث للموجات الكهرومغناطيسية يحمل فقط قيما معينة من الطاقة. او كما يقول افتراضه
E(vibration)= n * h *f
حيث f هو التردد و h هو ثابت بلانك الشهير اما n فهو عدد طبيعى ما. اى انه يحمل فقط القيم: 1 او 2 او 3 … الى اخره. بمعنى اخر ان الطاقة لاتحمل قيما متصلة ولكنها قفزات كمية. ومن هنا تأتى التسمية كلها للنظرية بنظرية الكم. فالطاقة فى المثال السابق قد تكون hf او 2hf ولكنها لا يمكن ان تكون قيمة فى المنتصف.
واذا عدنا الى الميكانيكا الكلاسيكية والبندول البسيط فمعنى هذا ان البندول يهتز عندما ارفعه 5 سم او مضاعفات هذا الرقم. بمعنى ان البندول سوف يهتز عندما ارفعه 10 سم. ولكن البندول لن يهتز عندما ارفعه 6 سم. وهذه فرضية مجنونة تخالف ما نعايشه فى حياتنا. فعندما ارفع سرعة السيارة من 90 كم فى الساعة الى 100 كم فى الساعة. فاننى امر عبر كل القيم فى المنتصف ولا اقفز فوقها كما يقول بلانك.
دعونى احاول ان اقرب فكرة بلانك بتشبيه. كلنا نعلم بالتليفونات المحمولة وبامكانية شحن الرصيد عن طريق بطاقات الشحن فلو تخيلنا ان معى تليفون محمول ولكنه بلا رصيد . وانا معى يورو واحد وبطاقة الشحن اللازمة قيمتها 10 يورو على الاقل. اذن فانا لن اتمكن فى الحديث هاتفيا وساضع اليورو و الهاتف المحمول امامى و استمتع بجمالهما ولكنى لن استطيع ان اجري مكالمة تليفونية واحدة. فقط اذا كان بحوزتى 10 يورو او 20 يورو او مضاعفات ذلك فسيكون بامكاني اجراء مكالمات تليفونية عن طريق شراء بطاقات شحن بالنقد المقوجود ثم اجراء الاتصالات الضرورية.
مثال اخر لنتخيل ان لدينا 3 تليفونات محمولة كلها فيها بطاقات تشغيل لشركات خدمات تليفونية مختلفة. فالتليفون الاول يستخدم خط شركة الفقراء وسعر بطاقة الشحن فيه 2 يورو والتليفون الثانى يستخدم خط متوسطى الحال وسعر بطاقة الشحن فيه 3 يورو. ثم خط شركة الاغنياء وسعر البطاقى فيه 11 يورو. ثم نتخيل ان بحوزتى 7 يورو واريد ان اجرى بها كلها مكالمات تليفونية. فكيف يمككننى ذلك؟ طبعا لن يمكنى ان استخدم ابدا خط الاغنياء. ولكنى سأشترى بطاقتين من شركة الفقراء وبطاقة من شركة متوسطى الحال. هذا المثال يوضح تماما لماذا لا تظهر الكارثة فوق بنفسجية عند درجات الحرارة المنخفضة. لان الطاقة المطلوبة تكون عالية جدا
لكن بواسطة هذين الفرضين وباستغلال خواصى الانتروبى استطاع بلانك ان يضع معادلته اللتى تؤدي الى نفس النتيجة اللتى نحصل عليها فى المختبر. فى النهاية يجب ان نقول انه لحسن الحظ فان بلانك لم يستمع لنصيحة استاذه سوى لفصل دراسى واحد ثم انتقل بعده لدراسة الفيزياء فى جامعة برلين!