-هل تقصد ب i ذلك العدد التخيلى اللذى هو الجذر التربيعى لسالب واحد؟
-نعم تماما
-بالطبع لا أعلم الاجابة. فانا بالكاد استسيغ ذلك العدد التخيلي. بل أكثر من ذلك لا أخفيك سرا فانا لا أعلم ما معنى ألا يكون الأس عددا صحيحا موجبا. فانا مثلا لا افهم ماللذي تعنيه القيمة 52.5 فما معنى ان اضرب الخمسة مرتين ونصف فى نفسها؟ انا استطيع ان اضرب الخمسة فى نفسها مرتين او ثلاثة وليس كسرا!
أن التقديم السابق يشى بهدفهنا الحقيقي اليوم. وهو ليس مجرد تقديم نتيجة السؤال فى العنوان فقط والا لأنتهينا من الموضوع فى أقل من ثانية. ولكن الهدف الحقيقي هو فهم عملية حساب الأس من الأساس. ولذا سوف نقوم اليوم بنزهة رياضية فى رياض التفكير المنطقي.
هناك خاصيتان تميزان الرياضيات وتجعلان منها سهلا ممتنعا. وهاتان الخاصيتان البسيطتان -ولكنهما غاليتان الثمن عند الكثير من الناس- هما التجريد والتعميم. المقصود بالتجريد ان تكون كل قضايا الرياضيات ونتائجها مجردة عن الواقع الحسى ومقصورة على المفاهيم الرياضية فقط. مثال للتجريد اجابة السؤال حول ماهية الأعداد. اما التعميم فهو الانطلاق من الحالات الخاصة الى الحالات العامة: مثل الانطلاق من ثلاثة أبعاد الي ثلاثين او ثلاثة ألاف بعد. وبالرغم من ان عقلنا البشرى لا يستطيع ان يتخيل ذلك مجسدا لكنه يستطيع ان يتعامل مع الأبعاد العديدة منطقيا. وموضوعنا اليوم ينتمى الى النوعية الثانية كما سنرى سريعا.
دعونا نرى تشبيها بسيطا: لا أعلم بوجود ارانب خضراء اللون -انا لست متخصص فى الأحياء- لكن ماذا لو رأينا ارنبا أخضرا؟ سوف نتعرف عليه فورا. فخضار اللون او بياضه ليست السمة الأساسية فى الأرنب. والعقل البشري سوف يتعرف عليه بأي لون . فدعونا نسأل السؤال الرئيس: مااللذي يجعل من الأرنب في حقيقة الأمر أرنبا!؟ مثال اخر هناك طاولات مختلفة الأشكال بعضها له ثلاثة قوائم وبعضها له أربعة قوائم وبعضها له أكثر من ذلك. بعض الطاولات شكلها مثلث والأخر مربع أو مستطيل او مستدير أو غير ذلك. واذا صمم فنان طاولة غير مسبوقة سنتعرف عليها فورا وسندرك انها طاولة. والعلم المختص فى السؤال حول ماهيات الأشياء نطلق عليه الاونتولوجي Ontololgy وهو مهم فى ميادين مختلفة كالفلسفة وانظمة المعلومات. فمحرك البحث جوجل سواء كتبنا عنده فندق او لوكاندة اوبنسيون او مكان للنوم مقابل أجر فسوف يفهم اننا نبحث عن فندق. فلنعود الى موضوع اليوم ونسأل السؤال المصيري: ماللذي يجعل العملية الأسية كأسمها؟!
دعونا ننطلق من العملية الخاصة 53 اللتى نعرفها جيدا لنرى ماللذي يميزها. نحن ننطقها خسمة أس ثلاثة. ونرى عددين: الاول هو الخمسة ونطلق عليه الاساس والعدد الثانى هو الثلاثة اللذي نطلق عليه الأس. ونلمس ان الاساس لا يزعجنا فى اي شئ فقد يكون كما يكون. فحتي لو كان علينا ان نحسب كرسي أس ثلاثة لما كان لدينا أي مشكلة!. علينا أن نضرب كرسى فى كرسي فى كرسى حتى نحصل على النتيجة المطلوبة. صحيح اننا لانعلم كيف نجري عملية ضرب كرسى فى كرسى لكن الطريق ينبغى ان يكون هكذا! فقط الأس عندما لا يكون عددا صحيحا موجبا هو ما يؤرقنا.
اذن كون الأس عددا صحيحا موجبا هو مايماثل كون الأرنب أبيضا. واذا اردنا تعميم عملية حساب الأس فعلينا ان نسأل عن السمات العميقة الكامنة خلف عملية حساب الأس. ودعونا نحاول ان نجد اجابة للسؤال المصيرى اللذى ذكرناه عاليا: ماللذي يجعل من عملية حساب الأس كذلك؟ الاجابة اللتى نكتشفها بعد قدر يسير من التأمل هي ان العملية الأسية هى عملية رياضية تحول من عمليات الجمع في الأس الى عمليات ضرب!. وهذا نستطيع ان نعبر عنه بالعلاقة التالية:
am+n = am . an
بل دعونا نسبق الاحداث ونقول ان أجابة السؤال فى الحوار عن معنى حساب 5 اس 2.5 أنها عملية ضرب خمسة أس 2 فى خمسة اس 0.5 !
52 . 50.5 = 52.5
لكن ما معنى حساب 5 أس 0.5؟ نستطيع ان نحلل ال 0.5 بدوره الى 0.25 + 0.25 ونواصل البحث من جديد وهكذا. وقد يظن البعض ان هذه العملية لانهاية لها واننا سنبقي ندور ونلف فى مكاننا. لكن هذا حكم متسرع فكما سنرى لاحقا نستطيع ان نحسم الامر سريعا.
وهناك قاعدة الثانية نحتاجها وهي تبدو جلية ولاتحتاج الي ذكر لكنى اصر على ذكرها صراحة. القاعدة الثانية تقول ان 5 اس 1 تساوي خمسة. او بمعني عام ان أي عدد أس واحد يساوى نفسه او:
a1 = a
هاتان القاعدتان هما جزأي مفتاح شفرة الحساب الأسي. ودعونا نرى عملية حساب الأس فى الضوء الجديد. ودعونا نبدأ بحساب العملية اللتى ليس لدينا معها مشكلة من الأساس وهى عملية حساب 5 أس ثلاثة
51+1+1 = 53
51.51.51 = 53
5.5.5 = 53
125 = 53
وكما نرى اننا طبقنا جزأى مفتاحي الشفرة وحصلنا على النتيجة المتوقعة تماما. لكن الفائدة اللتى جنيناها هي أننا تخلصنا من تصور أن الأس عبارة عن تكرار لعمليات الضرب لصالح صورة أعم وهى ان عملية حساب الأس تعنى تحويل الجمع في الأس الي ضرب. دعونا نعمم ذلك الأمر عندما يكون الأس صفرا أو عددا صحيحا سالبا أو كسرا أو عددا نسبيا عموما أو عددا غير نسبي أو عددا تخيلي أومركب!
وبالرغم من اننا نطمح الي تحقيق الكثير الا أن خطوات الحل ستبقي دائما ثابتة: سنبدأ دائما من قيمة أسية. ثم نحلل الأس الى أعداد مجموعة الى بعضها. أحد هذه الأعداد هو عدد يهمنا ان نحسب قيمة الأس بالنسبة له. ثم نحول عمليات الجمع فى الأس الى عمليات ضرب متلاحمة كما تقول القاعدة الاولى. بعد ذلك نقوم بالقسمة لنحصل على النتيجة النهائية اللتى نسعى وراءها.
دعونا نبدأ بالصفر حيث يعلم معظمنا ان 5 أس صفر تعطى النتيجة واحدا. لكن كيف يمكننا ان نثبت ذلك رياضيا؟ علينا فقط ان نتبع الخطوات السابقة ونفعل التالي
50+3 = 53
50.53 = 53
بقسمة طرفي المعادلة على 53 نحصل على
50 = 1
ودعونا نفعل نفس الشئ بالنسبة للأس السالب. فنعلم مثلا ان خمسة أس سالب اثنين تعطى قيمة موجبة تساوى 1/25 لكن كيف يمكننا ان نثبت ذلك رياضيا؟ علينا ان نتبع نفس الخطوات ونبدأ من القيمة خمسة اس صفر اللتى عرفناها توا ونحلل الصفر الى مجموع العددين 2 و سالب 2 لنحصل على النتيجة المرجوة أو:
1 = 50
1= 5-2+2
1 = 5-2 . 52
1/52 = 5-2
ثم دعونا نفعل نفس الأمر بالنسبة للكسور! فماذا عن حساب قيمة خمسة اس ثلث؟ نعلم ان النتيجة ستكون هى الجذر التكعيبى لخمسة لكن كيف يمكننا ان نثبت ذلك؟ علينا ان ننطلق من 5 اس واحد ثم نحول الواحد الى 3 مرات الثلث مجموع الى نفسه لنحصل على النتيجة المطلوبة أو كما يلي
5 = 51
5= 51/3+1/3+1/3
5 = 51/3 . 51/3 . 51/3
5 = (51/3)3
5√3 = 51/3
لكن ماذا عن حساب 5 اس 2/3 ؟ يمكننا ان نحول 2/3 الي 1/3 مجموعة الى نفسها مرتين
51/3+1/3= 52/3
51/3 . 51/3 = 52/3
2(51/3)= 52/3
2(5√3) = 52/3
أو عموما العلاقة العامة التالية:
(n√a)m = am/n وحيث أننا نعلم أن أي عدد عشري يمكن تحويله الى كسر فيكون معنى
5.5√5 = 51+1+1/2= 52.5
لكن ماذا عن الاعداد غير النسبية؟ فنحن كما نعلم أننا لانستطيع ان نعبر عنها فى صورة نسبة. المساعدة تأتي هنا من تعريف كانتور Cantor للأعداد الغير النسبية بدلالة الأعداد النسبية. فقد عرفها بانها متتالية من الأعداد النسبية نهايتها هى العدد الغير نسبي المطلوب. مثال للعدد جذر 2 المتتالية التالية
a(0)=1.0
a(1)=1.4
a(2)=1.41
a(3)=1.414
الى اخره
وبالتالي يكون قيمة 2√ 5 هي نهاية المتتالية
a(0)=51
a(1)=51.4
a(2)=51.41
a(3)=51.414
او ان 2√ 5≈ 51.414213562
الان نصل الى الأعداد التخيلية. لكن دعونا قبل ان نبدأ ان نقوم بتمهيد بسيط لا غنى عنه. فالاعداد المركبة توجد لكتابتها صيغتان رئيستان يجب ان نعرفهما ونتقن الانتقال بينهما فى مرونة لاعبي الجمباز. وكلتا الصيغتين تعتمدان على انه يمكن تخيل مستوي تقع فيه الأعداد المركبة جميعا. الصيغة الأول نطلق عليها الصيغة التحليلية او الكارتيزية وفيها نحلل العدد المركب بالنسبة الى محوري الاعداد الحقيقة والتخيلية مثال لهذا الصيغة العدد التالي
z=2 + 2i
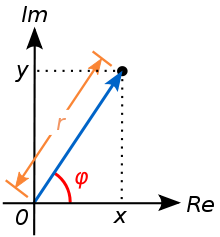
اما الصيغة الثانية ونطلق عليها الصيغة القطبية فهنا لانحلل العدد المركب بدلالة المحورين الحقيقي والتخيليى. لكننا نقوم اولا بتحديد المسافة بين العدد المركب ونقطة الصفر فى مستوي الأعداد المركبة. فاذا كانت المسافة مثلا 2 فاننا نكون حددنا نقاط محيط دائرة تبعد عن نقطة الصفر بالبعد 2. ويكون العدد اللذي نريد صياغته هو احد هذه النقاط. لكننا لم نحدده وحده تماما. ولتحديد العدد بمفرده تماما فاننا نحتاج الى قيمة اخرى بجانب نصف القطر وهي الزاوية اللتى يصنعها الخط الواصل بين موقع العدد ونقطة الصفر مع محور الأعداد الحقيقية الموجب. لذلك نعبر عن العدد المركب مرة اخرى عن طريق عددين يعبران عن المسافة والزاوية ونكتبهما هكذا: [r,a] وهناك طريقة اخرى للكتابة وهى reai اما عن سبب هذه الصياغة اللتى تحتوى على عدد أويلر فبرهانها ينبع من معادلة اويلر واللتى يطلق عليها جوهرة الرياضيات:
eai = cos(a) + sin(a) i
واترك لكم التأمل فى تحليل سر الربط بين الصياغتين.
مثال للصيغة القطبية هي صياغة العدد التخيلي i حيث اننا نعلم ان المسافة بينه وبين نقطة الصفر تساوي واحد والزاوية اللتى يصنعها موقع ذلك العدد بالنسبة لمحور الأعداد الموجبة تساوي قائمة او π/2 وبالتالي يمكننا ان نصيغ العدد i بالصورة التالية
[1,π/2]
الأن ننتقل الى الذروة وهى حساب الاس بالنسبة للأعداد المركبة. ومن اجل اتمام ذلك الهدف الطموح دعونا نتم ذلك فى ثلاث خطوات: الخطوة الاولي هى ان نحسب النتيجة بالنسبة لارقام خاصة ومختارة بعناية. الخطوة الثانية ان نعمم نتائج ماوصلنا اليه بشكل ما. ثم الخطوة الثالة وهي الخطوة النهائية وفيها نصل الى وصف العلاقة اللتى نريد ان نصل اليها. اذن دعونا نبدأ
الخطوة الأولى دعونا نبدأ بالاساس عبارة عن عدد أويلر e وبالأس ln2+3i وكما نري فان الأس فى الصيغة التحليلية. لذلك نستطيع أن نستغل القاعدة الاولي حيث ان الصيغة التحليلية الكارتيزية تحتوى على عملية جمع. والمفاجأة اننا ننتهى بدون مجهود يذكر الى عدد مركب جديد مصاغ بالصيغة القطبية.
eln2+3i = eln2 . e3i= 2e3i =[2,3]=result
وهنا يجب ان نعلق على ان اختيار الاساس بالقيمة e كان اختيار اساسيا لامحيد عنه من اجل اتمام هذه الخطوة بنجاح اما اختيار الأس فقد كان مجرد اختيار لسهولة الأرقام وسينجح أي مثال أخر بأي أس بخلاف الأس السابق لكن الأساس يجب ان يبقي e
الخطوة الثانية دعونا نعمم النتيجة السابقة. ولكننا سوف نعمم العملية العكسية وهى عملية حساب اللوغاريتم ! -ومعنى حساب اللوغاريتم وهو حساب الأس اذا كانت النتيجة النهائية معلومة وذلك بالنسبة للأساس e – ومن اجل ذلك نعيد الخطوات السابقة من الخلف الى الأمام فيجب ان نبدأ بعدد مركب فى الصياغة القطبية فتكون النتيجة في الصيغة التحليلية كالتالي:
ln[r,a] =lnr+ai
أو أن الجزء الحقيقى هو لوغاريتم المسافة r والجزء التخيلى هى الزاوية نفسها بدون أي تغيير. فدعونا نرى ذلك بالنسبة لحساب لوغاريتم العدد التخيلى i . فنصيغ i فى الصورة القطبية لنصل الى النتيجة التالية
ln(i) = ln[1,π/2] = ln(1)+π/2i = π/2i
وهذه النتيجة سنحتاجها لاحقا.
الخطوة الثالثة هى الخطوة النهائية وفيها سنجري العملية الأسية بالنسبة لأى رقمين مركبين wz بعد ان تعلمنا اجراءها عندما يكون الأساس عدد أويلر كما رأينا فى الخطوة الأولي. لكن ماذا عندما لا يكون الأساس ذلك؟ هناك حيلة نستطيع بواسطتها تحويل أي عدد مهما كان الى قيمة أسية يكون عدد اويلر هو الاساس فيها مثال على ذلل الحالات التالية
2 = eln2
i= elni
w=elnw
اذن يمكننا ان نحول القيمة اللتى نريد حسابها الى الصورة التالية eln(w))z. وهنا لابد ان نتذكر القانون الرياضى اللذي يعرف بحساب أس الأس وهو صياغته كالتالي.
(ab)c = abc
ومن المهم ان نذكر بأن هذا القانون سارى فقط بالنسبة للأعداد الحقيقية عندما تكون a قيمة موجبة. وهذا الامر ينساه الكثير من الناس أحيانا مما قد يسبب تناقضات كبيرة لهم. فاذن كان ذلك القانون ساريا ايضا بالنسبة للاعداد المركبة ستكون القيمة اللتى نريد حسابها هى كالتالي ezlnw وهو أمر تعلمنا اجراءه فى الخطوة الاولي. اذن السؤال هنا: هل يمكننا ان نبرهن قانون أس الأس بالنسبة للأعداد المركبة؟
الاجابة هى لا. اننا لا نستطيع ذلك! لكننا سنفعل شيئا أخر فنحن لا نحتاج لبرهنة هذه القانون. بل سنثبته بالتعريف. ودعونا نسأل السؤال المصيري مرة اخرى: ما معنى عملية حساب الأس بالنسبة للأعداد المركبةwz؟ الأجابة هى :ezlnw نقطة ومن أول السطر
ومع ان التعريفات الرياضية لاتبرر الا ان هذا التعريف نلحظ عليه ان ليس تعسفيا شاذا وليس حكم قراقوش كما يقول المثل الشعبي. لكن يمكن استلهامه من مد قوانين حساب الأس بالنسبة للأعداد الحقيقية على استقامتها.
اذن نعود الى السؤال فى العنوان ونستغل كل الحقائق السابقة لنصل الى النتيجة التالية:
ii = eiln(i) = ei.π/2 i = e-π /2
وهذا امر غريب فالنتيجة ليست كما توقع البعض وليست عددا تخيليا بل عددا حقيقا. وكما أن ضرب i في i يعطى عددا حقيقيا سالبا وهو سالب واحد فان i أس i تعطى عددا حقيقيا موجبا يساوى تقريبا 0.207879576
وهناك نقطة هامة جدا أغفلناها حتى الأن وهي أن قيمة حساب اللوغاريتم وقيمة حساب الأس بالنسبة للأعداد المركبة ليست نتيجة وحيدة ولكن هناك دائما عدد لانهائى من النتائج الممكنة. اذن لاجابة السؤال فى العنوان عدد لانهائى من الأجوبة. لكنها جميعها لفرط المفاجاة اعدادا حقيقية !