حساب الأحتمالات هو موضوع رياضي سهل ممتنع. فهو بسيط لأن قواعده واضحة وقوانينه بديهية جدا مع ان نتائجها ليست كذلك دائما. وهو فى نفس الوقت صعب لأمرين. الأول: هو أنه يحتاج لأن نصيغ أفكارنا بصورة بسيطة لكن فى نفس الوقت دقيقة جدا. فجمل على وزن انا أفهم لكنى لا أستطيع ان أعبر لا تغنى شيئا. والحقيقة انه من لا يستطيع ان يصف قضية ما كتابة بلغة فصحى سليمة فانه لا يفهمها. الأمر الثانى انه فى حساب الأحتمالات يجب ان يصوم المرء عن استخدام بديهته تماما ويلجأ لتطبيق القوانين بمنهتى التجرد. ولتأتى بما تشاء من النتائج.
وحساب الأحتمالات المشروطة هو ذروة مواضيع حساب الأحتمالات اثارة للارباك. ومثال للاحتمالات المشروطة تلميذ يريد ان يعرف ماهي احتمالات نجاحه فى اختبارات اخر العام بعد أن أتته معلومة انه قد نجح فى مادة الرياضيات. فاذا كنت الرياضيات تشكل مشكلة بالنسبة له فلاشك انه سيشعر بارتياح كبير ويشعر بان احتمالات نجاحه الكلية قد زادت.
وحساب الأحتمالات المشروطة يغطيه قانون يعرف باسم قانون بايز واللذي يحمل أسم مكتشفه توماس بايز Thomas Bayes اللذي أكتشف هذا القانون فى القرن الثامن عشر. ولتوضيح طريقة تطبيق هذا القانون سنمهد له أولا بأربعة نقاط نظرية. ثم نرى بعدها أمثلة مختلفة.
النقطة الأولي هي أن قيمة حساب الأحتمالات هى دائما قيمة تنحصر بين الصفر والواحد. فاذا كانت النتيجة صفر كان معنى هذا انه حدث مستحيل الحدوث. واذا كانت قيمته واحد فهذا معناه أنه حدث أكيد لا مناص منه. ولكنه يكون فى معظم الأحوال بين هاتين القيمتين. مثلا الأحتمال 0.5 يعنى ان هذا الحدث سوف يحدث فى نصف المناسبات اللتى ممكن أن يحدث فيها ولن يحدث فى النصف الأخر فى المتوسط.
النقطة الثانية هي أننا نحسب الأحتمالات دائما لأحداث وهذه الكلمة هى جمع “حدث” Event وهذا مصطلح رياضى سأستخدمه هنا على الدوام. كما أن العملية الكلية اللتى نحسب من أجلها الاحتمالات نطلق عليها “التجربة” Experiment وهذا أيضا مصطلح رسمي.
النقطة الثالثة هى قانون بايز نفسه. اللذي مفاده لحساب احتمال حدث أول بدلالة حدث ثان قد حدث بالفعل فعلينا أن نقسم قيمة أحتمال حدوث الحدثين الأول والثانى مجتمعين على قيمة أحتمال الحدث الثاني. فلنعود الى مثال التلميذ اللذي يقدر أحتمالات نجاحه فى الرياضيات ب 0.5 او 50% . واحتمالات نجاحه فى الأمتحانات جميعها طبعا لايمكن أن تزيد عن 0.5 لانها قيمة احتمالات نجاحه فى الرياضيات وحدها. ولنفرض أن احتمالات نجاحه الكلية هي 0.45 . فهو لا يخشى شيئا بخلاف الرياضيات سوى الفيزياء قليلا. فاذا علم التلميذ انه نجح فى الرياضيات اذن سيكون احتمال نجاحه الكلي يساوى قسمة احتمال نجاحه فى جميع المواد أو 0.45 على أحتمالات نجاحه فى الرياضيات وهي 0.5 فتصبح أحتمالات نجاحه الأن هى 0.9 أو 90%! وصياغة القانون الرياضية هى كالتالي:
p(C|A)=p(C&A)/p(A)0
حيث ترمز “P” الى الأحتمال وهى مشتقة من الكلمة الأنجليزية Probability و “C”هى الحدث الأول و “A” هى الحدث الثانى والشرطة الرأسية “|” معناها بشرط حدوث و هذه العلامة “&” هى حرف العطف “و”
النقطة الرابعة تتعلق بحساب الاحتمالات فى البسط والمقام فى القانون السابق فنحن فى معظم الاحوال لن نتلقاها هدية كما كان الحال فى مثال التلميذ السابق. لكن علينا ان نحسبها بطريقة ما. وهناك تقنية تمكننا من ذلك وهى تقنية التخطيط الشجرى Tree diagram. وفيها نكتب كل الاحداث ممكنة الحدوث كأفرع شجرة. وفلسفة هذه التقنية نعرفها من خلال المتاجر الرقمية على صفحات الأنترنت بل وفي الحياة العامة عموما. فاذا تخيلنا مثلا اننا نريد أن نشترى سيارة فذهبنا الى صاحب معرض سيارات عنده 50 سيارة. ولكى يسهل عليه وعلينا البحث. يسألنا سؤالين. الأول ما هو نوع السيارة اللذي نريده؟ اتوماتيكى أو نقل يدوي؟. وبفرض أنه يمتلك 25 سيارة نقل يدوي و25 نقل أوتوماتيكى فبعد أجابة هذا السؤال يصبح عندنا 25 سيارة فقط. ثم يأتى السؤال الثاني اى لون نريده. فهناك 5 ألوان لديه: أحمر أخضر ازرق أسود أو باقي الألوان حيث أن صاحب المعرض يمتلك 5 سيارت من كل لون ومن ذات طريقة النقل. واذا اردنا شراء سيارتين فاننا بعد أن ننتهى من أختيار السيارة الأولي نعيد نفس الخطوات بالنسبة للسيارة الثانية. وستتضح هذه التقنية فى الأمثلة التالية لكننا ننوه اننا سنستخدم لونين للتوضيح: اللون ألاحمر للمسارات الداخلة فى حساب البسط واللون الأخضر لتحديد مسارات حساب المقام. وسنكتب بجوار كل فرع الاحتمالات الخاصة به. ولحساب أحتمال مسار بالكامل من أقصي اليسار الى أقصى اليمين نضرب الأحتمالات المتوالية على فرع الشجرة حتى ننتهى منها جميعا.
المثال الأول
وقد رأينا هذا المثال المرة الماضية وحسبناه بالأرقام وبالتفكير المنطقى . لكننا اليوم سنتعامل معه من خلال قانون بايز. لكن فى البداية نعيد صياغة المثال مرة اخرى. فهو يقول انه فى حملة مرورية هدفها الكشف اذا كان قائدوا السيارات يتعاطون مواد مخدرة أم لا يتم أستخدام جهاز دقته 99%. ثم أعطى الجهاز نتيجة أيجابية عند أحد قائدي السيارات فما هو أحتمال أن يكون فعلا متعاطيا للمخدرات اذا علمنا أن نسبة التعاطى فى هذه المدينة تبلغ 1%؟
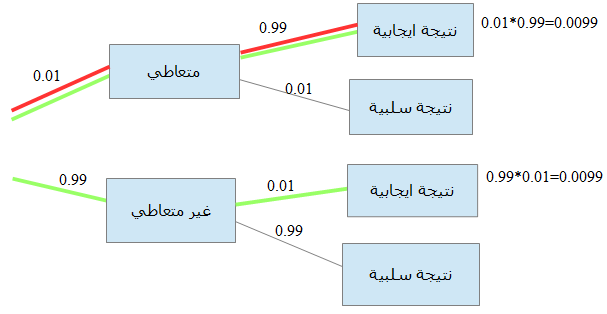
اذن اذا اردنا تطبيق بايز فالحدث C اللذي نريد أن نحسبه هو أن يكون قائد السيارة متعاطى للمواد المخدرة. اما الحدث A اللذي وقع هو أن الجهاز يقول ذلك. اذن علينا ان نرسم التخطيط الشجرى لتلك التجربة. نعلم أن هناك اولا عن أخر 4 احتمالات ممكنة:
1 أن يكون قائد السيارة متعاطيا لمواد مخدرة والجهاز يقول ذلك
2 أن يكون قائد السيارة متعاطيا والجهاز لا يقول ذلك
3 ان يكون قائد السيارة ليس متعاطيا لكن الجهاز يقول أنه متعاطيا
4 أن يكون قائد السيارة ليس متعاطيا ويقول الجهاز أيضا أنه ليس متعاطي
وهنا نرى كما كان فى مثال معرض السيارات حيث كان هناك معياران: لون السيارة ونقل الحركة الميكانيكى هنا يوجد أيضا معياران: هل قائد السيارة متعاطى أولا ثم ماذا يقول الجهاز. اذن وكما يقول قانون بايز فعلينا ان نحدد قيمتى احتمالين: الأول هو أن يكون قائد السيارة متعاطي وأن يؤكد الجهاز ذلك. وكما نرى فى الرسم هناك مسار واحد يؤدي الى تلك النتيجة. وهذا المسار يحمل الاحتمال 0.0099 ثم احتمال ان يعطي الجهاز نتيجة ايجابية ونجد لذلك مساران لكل منهم الأحتمال 0.0099. وبذلك يكون الاحتمال اللذى نريده يساوي 50%.
المثال الثاني
قبل 20 عاما تقريبا . تحديدا فى عام 1997 ظهر مقالان لكاتبين أمريكى وأنجليزي حول الأحتمالات المشروطة في غاية الغرابة. ودعونا نرى أولا المثال اللذي كتبه الأنجليزي ايان ستيوارت Ian Stewart.
جيرانك الجدد هم عائلة من رجل وزوجته ولديهما طفلان. أنت تعلم أن أحد الطفلين بنت. فما هو أحتمال أن يكون الطفل الثانى بنت أيضا؟
دعونا نفكر بصوت عال. بما أن الطفل الأخر اما ان يكون ولد أو بنت وأحتمالات الجنسين متساوية تقريبا. اذا احتمال الطفل الثانى بنت هو 50%. للأسف الأجابة خاطئة. ودعونا نرى ذلك فى ضوء تطبيق قانون بايز.
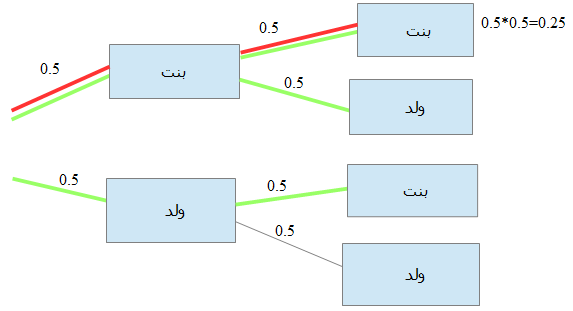
الحدث اللذي نريد ان نحسبه هو كون الطفلين بنتين بدلالة أن احد الطفلين بنت على الأقل. اذن دعونا نرسم شجرة الأحتمالات ودعونا نرى أى المسارات تقود الى ان الطفلين بنتين. والأمر يشبه مثال معرض السيارات. لكن هنا يوجد معيار واحد يتحكم في النتيجة وهو جنس الطفل ذكر أم انثى. كما أنه يوجد أختلاف ثان. فى مثال السيارة كنا نريد اختيار سيارة واحدة لكننا هنا نريد اختيار طفلين. وكما سبق وقلنا بعد السؤل عن جنس الطفل الأول سنسأل عن جنس الطفل الثاني. نجد ان هناك مسار واحدا للنتيجة بنتين. بينما المسارات اللتى تؤدي الى كون احد الطفلين بنت ثلاثة وقيمة احتمال كل مسار من المسارات السابقة يساوي ضرب 0.5 في 0.5 أو 0.25 اذن قيمة البسط هى 0.25 بينما قيمة المقام 0.75 وتكون النتيجة النهائية هى ان أحتمال كون الطفل الثانى بنتا يساوي الثلث!
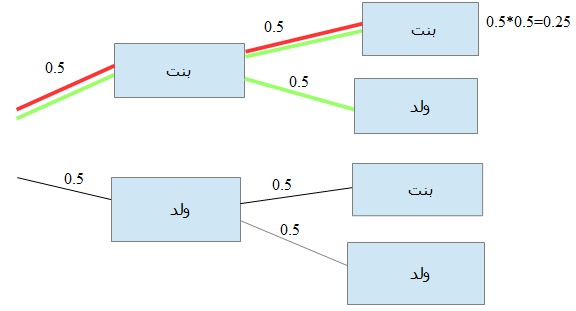
دعونا نغير فى المثال السابق قليلا. نحن نعلم الأن ان الطفل الأكبر هو بنت فما أحتمال ان يكون الطفل الثانى بنت أيضا؟. هل الأمر سيان؟ كلا فالان ومن شجرة الاحتمالات نرى ان المسارات اللتى تؤدي ان الطفل ألأكبر هو بنت مساران فقط. واحتمال كون الطفل الثانى بنتا هو النصف فقط!
اذن فكما نقول دائما انما الرياضيات صياغة. والصياغة فى الحالة الثانية تختلف عنها فى الحالة الاولي وحساب الاحتمالات المشروطة يتوقف على كمية المعلوات اللتى نعلمها أو بمعنى أحري اللتي نجهلها عن تفاصيل الموضوع. وعبارة ان الطفل الأكبر بنت تحتوي العبارة الأولى بداخلها وهي ان أحد الطفلين بنت. لكن العبارة الأولى لا تحتوي العبارة الثانية بداخلها! وفي الحالة الثانية حصلنا على صفة فارقة تفرق بين الطفلين وهى الطفل الأكبر فلا يمكن أن يكون الطفلان أكبر فى نفس الوقت.
المثال الثالث
كتب الأمريكى روبرث ماثيوز مقالا شيقا جدا عام 1997 في مجلة ساينس science حول الأحتمالات المشروطة. وكما نعلم الأن ان قيمة احتمال الحدث المشروط تختلف فى العادة عن قيمة احتمال الحدث نفسه. فقد تكبر وقد تصغر. والسؤال اللذي أهتم به ماثيوز هو ماهى الشروط اللتى يصبح عندها الأحتمال المشروط أكبر من الأحتمال ألاصلي؟ ومتى يكون أقل؟ وقد أستطاع ماثيوز من تكوين علاقة بسيطة توضح هذا الأمر. ولن أثقل عليكم بالبرهان هنا. وخلاصة ما وجده ماثيوز أن احتمال الحدث المشروط “C|A” يكون أكبر من أحتمال C فقط عندما يكون حساب الأحتمال المشروط “A|C” أكبر من أحتمال الحدث المشروط -’A|C- حيث أن ’C أو C شرطة تعنى عدم حدوث C . وقد يبدو أن هذا امرا حسابيا مملا لا معنى له. لكن اننتظروا حتى ننقل ذلك الى التطبيقات العملية.
هناك مثلا متهم ونحن نريد ان نعرف ماهى احتمالات أن يكون مذنبا. واذا فرضنا الأن انه قد أعترف بجرمه فهذا هو الحدث A فهل تصير أحتمالات ان يكون مذنبا أكبر بعد أعترافه. اجابة ماثيوز ليس ذلك بالضرورة. احتمالات ادانته تزيد فعلا فى الحالات اللتى تكون فيها احتمالات أعتراف المذنب أكبر من أحتمالات أعتراف الغير مذنب! لكن أليس هذا أمر طبيعيى؟ فلماذا يعترف غير المذنب؟ الأجابة انه فى جرائم الأرهاب والجرائم اللتى يقترفها عتاة المجرمين على الأرجح يصمد هؤلاء المجرمون امام التحقيقات ولا يعترفون بأى شئ يدينهم وعلى الأرجح ان ينهار برئ مع ضغط التحقيقات. مثال اخر عكسي جرائم الأعتداءات الجنسية على الأطفال. ففى كثير من الأحوال اللتى يتم فيها أعتداء جنسى على طفل فانه يقدم شهادة تدين شخصا ما ثم يتراجع ويسحبها. فتراجع طفل عن شهادة لا تزيد احصائيا من براءة المتهم.
بل الأكثر من ذلك نعلم انه بتعدد القرائن تزيد احتمالات ادانة متهم. لكن ماثيوز يقول لا. فاذا كانت هناك قرينة س ثم ظهرت قرينة ص فليس بالضرورة أن يصبح المتهم احصائيا اكثر قربا للذنب. وهذا بشكل ما يذكرنى بنظرية الكم حيث قد يتداخل ضوء مع ضوء أخر فتكون النتيجة ظلام. فيقول قانون حساب الأحتمالات المشروطة تزيد احتمالية ذنب المتهم فقط اذا كان أحتمال حدوث ص بشرط حدوث س وكان المتهم مذنبا أكبر من أحتمال حدوث ص بشرط حدوث س وكان المتهم غير مذنب. بل وترتيب حدوث القرائن يصنع أيضا أختلافا. فمثلا اذا كانت هناك قرينتان وهما اعتراف متهم وظهور جثة فى جريمة قتل. فالامر يختلف ان اعترف المتهم وبناء على اعترافه ظهرت الجثة. أو ان الجثة قد ظهرت اولا ثم بعدها أعترف المتهم. فى الحالة الأولي الأتهام أقوى.