هيرمان مينكوفسكي هو بروفيسور للرياضيات و الفيزياء كان يعمل بجامعة زيورخ في سويسرا في نهاية القرن التاسع عشر وبداية القرن العشرين حيث كان البرت اينشتاين من ضمن طلابه اللذين تتلمذوا على يديه في تلك الفترة . ولم يكن انطباع مينكوفسكي عن اينشتاين في تلك الفترة ايجابيا. فكان مينكوفسكي يري في اينشتاين مثالا للطالب الكسول اللذي يحرص على التزويغ من المحاضرات اكثر من حرصه على حضورها. ولكن رأي مينكوفسكي في اينشتاين تغير تماما بعد اكتشاف اينشتاين للنظرية النسبية الخاصة. وصار مينكوفسكي من اكثر المتحمسين لهذه النظرية و المدافعين عنها. بل أنه طور رياضيات خاصة بالنظرية النسبية اللتي اكتشفها تلميذه.
كما نعلم ان تحويلات لورنتر تحمل الصورة التالية
[latex]x1 =(x -vt)/\sqrt{1-v^2/c^2}[/latex]
[latex]t1 =(t -xv/c^2)/\sqrt{1-v^2/c^2}[/latex]
وباستخدام رياضيات بسيطة نستطيع ان نتوصل الي ما توصل اليه مينكوفسكي. فبطرح مربع المعادلة الثانية مضروبة في مربع سرعة الضوء من مربع المعادلة الاولي نحصل على المعادلة التالية:
[latex]x1^2 – c^2t1^2 = x^2 – c^2t^2[/latex]
ويمكنكم تجريب هذا بانفسكم كتمرين رياضي لن يستغرق اكثر من 10 دقائق من وقتكم
هل كان هذا كل شئ؟ تقرييا!! مع زيادة ان مينكوفسكي اثبت الصورة العامة للقانون. حيث ان المعادلة السابقة تعبر عن الحركة بسرعة منتظمة موازية للمحور x اما الصورة العامة للحركة في اي اتجاه فهي كالتالي
[latex]x1^2 + y1^2 +z1^2 -c^2t1^2=x^2+y^2+z^2 -c^2t^2[/latex]
وقد يسال انسان ما هو الفارق بين هذه المعادلة و تحويلات لورنتر السابقة. الاجابة ان هناك 3 فوارق رئيسة بين هذه المعادلة وبين تحويلات لورنتر
الفارق الاول اننا تخلصنا من السرعة النسبية v تماما وحصلنا على علاقة عامة جديدة تسري بين اي مجموعتي اسناد تتحركان بالنسبة لبعضهما البعض في خط مستقيم بسرعة منتظمة بغض النظر عن السرعة النسبية ذاتها.
الفارق الثاني اننا عن طريق هذه المعادلة:
[latex]r^2 = x^2 + y^2 +z^2 – c^2t^2[/latex]
نحصل على قيمة ثابتة تتفق عليها جميع مجموعات الاسناد باجراء قياسات داخلية. فكما نعلم ان مجموعات الاسناد المختلفة تختلف في قياساتها للاطوال وللزمن وللكتل. و لاتتفق الا على سرعة الضوء و على هذه القيمة اللتي حصلنا عليها من المعادلة السابقة.
الفارق الثالث هو اننا نستطيع عن طريق هذه المعادلة الحصول على ما يعرف باسم الزمن الخاص. فكما نري ان الوحدة اللتى تعبر عن r هي المتر. اي ان r هي مسافة. فاذا قسمنا هذه المسافة على سرعة الضوء c حصلنا على ما يعرف باسم الزمن الخاص و اللذي يلعب دورا هاما في توضيح معضلة التوأم اللتى قد نتعرض لها لاحقا ان شاء الله
ولم يكتف مينكوفسكي عند هذا الحد بل انه تأمل فيما وراء هذه المعادلة الجامدة. ماذا يمكن ان يفهم الانسان فيما وراء هذه المعادلة؟
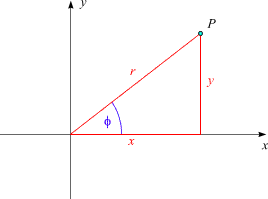
كما نعلم من الهندسة التحليلية انه اذا كان لدينا فضاء ثنائي الابعاد او بتعبير اخر مستوي ممتد يحتوي على محوري اسناد x و y و يتلاقيان في نقطة الاصل O وفرضنا ان هناك نقطة اخرى P ذات احداثيات x و y فيكون مربع المسافة بين هاتين النقطتين كما تقول نظرية فيثاغورث
[latex]r^2 = x^2 + y^2 [/latex]
و اذا عممنا هذه القاعدة على فضاء ثلاثي الابعاد اي يحتوي على المحاور x وy و z نجد ان مربع المسافة هي:
[latex]r^2 = x^2 + y^2 +z^2 [/latex]
وهذه المعادلة تشبه الى حد كبير معادلة مينكوفسكي اذا الغينا المقدار [latex]c^2t^2[/latex] .و اذا راعينا ان c هي سرعة الضوء و t هو الزمن وحاصل ضرب السرعة مع الزمن يعطي مسافة أو طول. اي ان هذا المقدار يمكن ان يعبر عن بعد رابع. وهنا نلمس براعة مينكوفسكي الرياضية حين قال اذا تعاملنا مع الزمن المضروب في سرعة الضوء كانه محور رابع. ولكنه محور ذو اعداد تخيلية فسنحصل على المعادلة :
[latex]s^2 = x^2 + y^2 +z^2 – c^2t^2[/latex]
والرقم التخيليي في الرياضيات يعني مضاعفات الجزر التربيعي لناقص واحد وهذا يفسر اشارة الناقص الاخيرة في المعادلة.
و ادخل مينكوفسكي تعبيرات فيزيائية جديدة فتخلي عن تسمية O و P بالنقاط ولكنه سماهما حدثين. والحدث يعبر عنه باربع ارقام تمثل الاحداثيات المختلفة. الاجداثيات الثلاثة الاولي للمكان و الاحداثي الرابع للزمن. و ادخل مينكوفسكي تعبير الزمكان وقصد به هذا الفضاء رباعي الابعاد وعبر عن البعد الزمكاني بالمعادلة السابقة.
و هناك نقطة اخرى يجدر الاشارة اليها وهي انه اذا فترضنا ان هناك مجموعتين اسناد في فضاء ثنائي الابعاد و تشتركان في نقطة الأصل O ولكنهما تميلان بزاوية بالنسبة لبعضهما البعض. فنجد العلاقة التالية سارية. لان طول الاجسام يبقي ثابتا في النظم الاحداثية المختلقة
[latex]r^2 = x^2 + y^2 = x1^2 + y1^2 [/latex]
و اذا افترضنا ان الفضاء كان ثلاثي الابعاد لوجدنا العلاقة التالية سارية
[latex]r^2 = x^2 + y^2 +z^2 = x1^2 + y1^2 +z1^2[/latex]
وبالمثل في فضاء رباعى الابعاد وبمحور تخيليى للزمن تكون العلاقة التالية هي السارية
[latex]r^2 = x^2 + y^2 +z^2 – c^2t^2 = x1^2 + y1^2 +z1^2 – c^2t1^2[/latex]
ومن هنا يمكن ان نري ان اي جسم يتحرك بسرعة ما يظهر لراصد يقف في مجموعة اسناد اخري كما لو كان هذا الجسم المتحرك مائلا
النقطة الاخيرة في هذا الموضوع هي اني احب ان اؤكد على ان الابعاد الاربعة موضوع اليوم ليست الا الابعاد المكانية الثلاثة اللتى نعرفها كلنا و البعد الرابع هو الزمن المعروف لدينا بشكل اكثر من جيد. ولربما توقع بعض القراء عند قرأتهم عنوان موضوع اليوم اني ساحلق بهم في جو اسطوري واني سوف اكشف لهم مستورا عظيما. ولكنى للاسف مضطر لان اخذلهم. فهذه الابعاد الاربعة تمثل لنا روتينا يوميا. فقط عندما تكون الابعاد خمسة او اكثر تبدأ الاثارة و التكهنات عن كنه هذه الابعاد الاضافية. ولكن النظرية النسبية لا تحتوي الا على اربعة ابعاد فقط. وربما تكمن المشكلة في ان مداركنا لا تتعامل مع كل الابعاد بنفس الكيفية. فمداركنا تستطيع استيعاب الابعاد المكانية بكل يسر فنحن نستطيع ان نري اي نقطة في المكان و النقاط اللتي وراءها والنقاط اللتي امامها. اما الزمن فأننا نستطيع ان ندرك اللحظة الحاضرة فقط و لانستطيع ان ندرك ما هو امام هذه اللحظة ولو فعلنا لرأينا المستقبل كما اننا لا نستطيع ان نري ما خلفها ولو فعلنا لرأينا الماضي. لأنه هو ايضا غيب بالنسبة لنا.