نصل اليوم  الى نظرية المركز الرابع وهي نظرية تنتمي الى ميدان الهندسة الفراغية وتقول ان عدد الاجسام الافلاطونية خمسة. وقد برهن هذه النظرية الاغريقي الاثيني ثياتيتوس Theaetetus اللذي عاش في الفترة مابين 417 الى 369 قبل الميلاد.

والسؤال الاول اللذي قد يطرح نفسه ما هي هذه الاجسام الافلاطونية؟ ولأجابة هذا السؤال لابد ان نستدعى في مخيلتنا المضلعات المنتظمة كالمثلث المتساوي الاضلاع او المربع او الخماسي المنتظم او السداسى المنتظم الى اخر هذه الاشكال المنتظمة اللانهائية حتى نصل في نهاية الأمر الى الدائرة اللتى تعتبر مضلعا منتظما ذا عدد لانهائي من الاضلاع . وما يميز كل هذه المضلعات المنتظمة أن كل اضلاعها متساوية في الطول كما ان زواياها متساوية ايضا. كما ان بامكاننا ان نرسم دائرة تحتوي على هذه الاشكال وبحيث يمر محيطها  باركان هذا المضلعات المنتظمة.  وكما سبق وذكرنا ضمنيا فان هناك عدد لانهائى من تلك المضلعات المنتظمة. ولذلك فأن بامكاننا ان نرسم مضلع منتظم ذا مليون او حتى مليار ضلع ولاتوجد اي مشكلة في ذلك.

والان ننتقل من حالة المستوي او الفضاء ذي البعدين الى الفضاء ذي الثلاثة ابعاد. فهل توجد اجسام فراغية منتظمة في الفضاء الثلاثى الابعاد كما توجد مضلعات منتظمة في الفضاء الثنائى الابعاد؟واجابة السؤال هي نعم وهذه الاجسام الفراغية المنتظمة في الفضاء الثلاثى الابعاد واللتى تمتلك عددا محدودا من الاضلاع هي الاجسام الافلاطونية. وربما يقفز الى مخيلتنا فورا اشكال مشهورة كالكرة أو المكعب فهي بالتاكيد اجسام منتظمة في الفضاء الثلاثى الابعاد.

لكن في البداية اود ان ابين ان الكرة ليست جسما افلاطونيا. صحيح انها جسم منتظم و لكن عدد اضلاعها  يعتبر لانهائي. و الاجسام الافلاطونية هي اجسام منتظمة ذات عدد محدود من الاضلاع.اذن يتبقى لنا المكعب. فهل يوجد بجوار المكعب اجسام افلاطونية اخري؟

الاجابة هي  مرة اخرى نعم. وهذه الاجسام معروفة مند عهد الاغريق. فالاغريق كانوا امة  هندسية بامتياز فقد اهتموا اهتماما عجيبا بعلم الهندسة وبحثوا فيه بشكل ضخم واولوا عناية كبيرة بالاجسام الافلاطونية . وقد درس فيثاغورث 4 اجسام افلاطونية بشكل مستفيض. وهذه الاجسام هي:

رباعى الاوجه

1 رباعى الاسطح المنتظم Tetrahedron وهو عبارة عن هرم ذي اربعة اسطح هي كلها مثلثات مثساوية الاضلاع.

مكعب

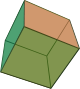
2  المكعب hexahedron او cube وهو جسم له 6 اسطح هي عبارة عن مربعات متساوية

ثمانى الاوجه

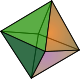
3  ثمانى الاسطح المنتظم Octahedron وهو جسم له 8 اسطح عبارة عن مثلثات متساوية الاضلاع وهو عبارة عن هرمين ملتصقين عند قاعدتهما المربعة

والاشكال الثلاثة الاولي هي اشكال تهم الكيميائيين بشكل خاص. لان كل  البلورات المعروفة تصطف ذراتها على اركان احد هذه الاشكال الثلاثة السابقة نظرا لما تمتاز به هذه الاشكال  من صفات هندسية مميزة وتناسق وثبات في الابعاد.

اثنا عشرى الاوجه

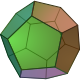
4 الاثنى عشرى الاسطح المنتظم Dodecahedron وهو عبارة عن جسم له اثنا عشر سطح هي كلها عبارة عن مخمسات منتظمة

وهناك شكل خامس لم يعرفه فيثاغورث ولكن ثياتيتوس صاحب نظرية اليوم هو اللذي اكتشفه. وهذا الشكل الخامس هو:

عشرونى الاوجه

5 العشرينى الاسطح المنتظم Icosahedron وهو عبارة عن جسم له 20 وجها هي كلها عبارة عن مثلثات متساوية الاضلاع.

كرة القدم هي عشرون وجهي مشطوف

و الجسمين الافلاطونيين الرابع و الخامس يهمون بصفة خاصة عشاق لعبة كرة القدم. لانهما اوحيا بتصميم شكل  كرة القدم الرسمية الحالي. وهو شكل يعرف تحديدا بعشرينى الوجوه المشطوف

وقد استغل الفنانون والرسامون ايام عصر النهضة امثال دافنشى هذه الاجسام الافلاطونية الخمسة لما فيها من انسجام وتناغم في رسم لوحاتهم. كما ان هذه الاشكال تهم صناع النرود حيث ان الارقام المطبوعةعلى اوجه حجر نرد على شكل جسم افلاطوني تحمل كلها نفس احتمالات الظهور. ويقال على النرد في هذه الحالة انه سليم او عادل.

ولكن لماذا وصفت هذه الاجسام بالافلاطونية مع ان افلاطون ليس مكتشف هذه الاجسام؟ الاجابة لان افلاطون اهتم جدا بهذه الاجسام وعنى بها ضمن فلسفته ليس فقط بسبب صفاتها الهندسية البديعة بل لانه اعتبرها ترمز الى العناصر الاولية: النار و الماء و الارض و الهواء. فرباعى الاوجه Tetrahedron يشبه باركانه المدببة النار بينما يشبه العشرينى الاوجه Icosahedron بحوافه الملساء الماء ويشبه المكعب الارض بينما يشبه ذو الثمانى اوجه Octahedron الهواء.ولم يهتم افلاطون بذي الاوجه الاثنى عشر Dodecahedron ولكن في العصور الوسطى تم اعتباره يرمز الى المادة اللتى تتكون منها الاجرام السماوية!!

وحيت ان اجواء اليوم اغريقية بامتياز. نضيف ان الكلمات   tetra و hexa و octa و dodeca و icosa تعنى بالاغريقية الاعداد 4 و6و 8 و 12 و 20 .

نعود مرة اخري الى نظرية اليوم فقد اثبت ثياتيتس انه لاتوجد أي اجسام افلاطونية اخرى بخلاف الاجسام الخمسة المذكورة. ثم احب ان اوضح ماهي الاسس و الشروط الرياضية اللتى يجب ان تتوفر في جسم فراغى حتى نقول انه جسم منتظم . في الحقيقة ان الجسم يكون منتظما عندما تتوافر فيه الشروط الثلاثة التالية:

شكل محدب

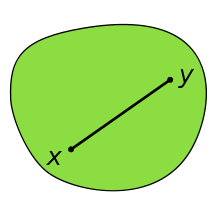
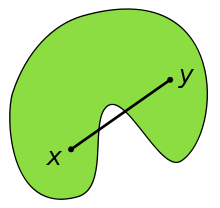
1 ان يكون الجسم محدبا . والجسم المحدب هو الجسم اللذي يقع اي خط بصل بين نقطتين فيه في داخل هذا الجسم بالكامل

2 ان تكون جميع اسطح هذا الجسم مضلعات منتظمة ولها نفس عدد الاضلاع. فمثلا اوجه المكعب كلها مربعات اي عدد الاضلاع فيها 4 واوجه الرباعى الاوجه Tetrahedron كلها مثلثات متساوية الاضلاع و عدد اضلاعها ثلاثة بينما اوجه الاثنى عشرى الوجوه Dodecahedron كلها مخمسات منتظمة و عدد اضلعها 5

3 تتقاطع عند اركان هذه الاشكال نفس العدد من من الحواف. ففى حالة المكعب يلتقى عند كل ركن 3 حواف. بينما بالنسبة للثمانى الوجوه يلتقى عند كل ركن 4 حواف.

في النهاية نري انه من الطبيعى ان يكون لنظرية اليوم مكانا بين النظريات الاكثر جمالا. فاولا  هي تتعلق باجسام اعتبرها

شكل غير محدب

الفنانون و الفلاسفة السابقون و الحالون رموزا للجمال. وثانيا فان هذه النظرية تحمل مفاجأة لطيفة فربما كان الاقرب للتوقع ان عدد الاجسام الافلاطونية يتخطى الخسمة اجسام. وثالثا فاننا نعلم ان الخيال البشري هائل ولاحدود و لا نهاية له ولكن نظرية اليوم تضع حدودا وقيودا لهذا الخيال وتنص على انه مهما حاول الانسان ان يتخيل اجساما منتظمة بخلاف الخمسة المذكورة عاليه فانه سيفشل. فهنا العقل البشري يضع حدودا للخيال للبشري.