شغلتنا جائحة كورونا فى الاونة الاخيرة. فانها بلا شك قد أنتشرت وتننشر بسرعة مرعبة عبر اصقاع الكرة الأرضية. وطبعا القارئ يدرك أن هذه الازمة تتطلب جهد المتخصصين في الميادين المتعددة. فبلا شك ان الازمة طبية تتعلق بالقطاع الصحي. لكن من الخطأ الكبير ان يتم التعامل مع هذه الازمة فى اطار ذلك التخصص فقط. فهذا الشأن لا يخص الاطباء وحدهم اللذين يداوون المرضى ولكنه يهم ايضا العلماء المتخصصين فى دراسة الفيروسات. حيث ان سبب هذا الازمة هو فيروس ينتمى الى عائلة كورونا ويسبب المرض المعروف باسم كوفيد 19. وهذه الازمة تتطلب ايضا الرياضيين اللذين يضعون النماذج الرياضية اللتى تصف انتشار ذلك الفيروس. وهذا الجانب هو جانب هام جدا لا يستطيع الاطباء ان يقوموا به حيث أن طبيعة الرياضيات بعيدة عن تخصصهم الاصلى. كما ان هذه الازمة تخص السياسيين ورجال الأقتصاد. حيث ان لهذه الازمة تبعات هائلة على حياة الناس والمجتمعات. مما يدعو الى تدخل السياسيين بصورة حكيمة للخروج من هذه الازمة بأقل قدر من الخسائر.
انا لست متخصصا فى الطب وليست لى دراية بعلم الأحياء. لكن لى بعض الاهتمام بالمواضيع الرياضية. ومن هنا أود ان اعرض عليكم كيف يتعامل الرياضيون مع هذه الحالات. وأود ان ابسط بعض النماذج الرياضية المستخدمة في تلك الظروف وان اقدم لكم نبذة عن رياضيات الاوبئة.
وسوف اقوم اليوم بعرض نموذج مبسط جدا لوصف انتشار الاوبئة. وفى الموضوع القادم ساقوم بعرض نموذج اخر أكثر تعقيدا. ولكنى احب ان انوه ان الهدف هنا ليس عمل توقعات او تنبؤات لما سوف يئول اليه الحال. ولكن الهدف هو عرض كيف يتم تعامل الرياضيين مع تلك المواضيع بصورة مبسطة للغاية.
لذلك سنستعرض اليوم موضوع النمو فى الرياضيات. وقبل ان نبدأ احب ان انوه ان النمو هنا مصطلح رياضى يختلف عن المعنى اللغوي الشائع. فالنمو عندنا قد يكون زيادة او نقصا بان يكون النمو سالبا. في حين ان المصطلح اللغوي يوحي ان النمو زيادة ولا يحتمل النقصان.
وهناك نقطة اخرى احب ان اشير اليها. وهي ان نقطة البداية فى كل النماذج اللتى سوف نتعامل معها ستكون سرعة حدوث النمو وليس النمو نفسه مباشرة. ومن لهم دراية بالرياضيات يعلمون ان هذا كناية عن حساب تفاضل النمو. اللذي نطلق عليه احيانا تفاضل واحيانا معدل التغيربالنسبة للزمن. وانطلاقا من نقطة البداية هذه وللوصول الى النمو نفسه لابد وان نجري ما هو عكس لعملية التفاضل. اى اننا سوف نجرى عملية تكامل. ولكننى هنا لن اتطرق الى التفصيلات الرياضية اللتى سوف تكون معقدة لغير المتخصصين.
وسوف نتعرض اليوم لاربعة نماذج اللنمو: وهي النمو الخطي والنمو الأسى والنمو المحدود والنمو اللوجيستي
النمو الخطي
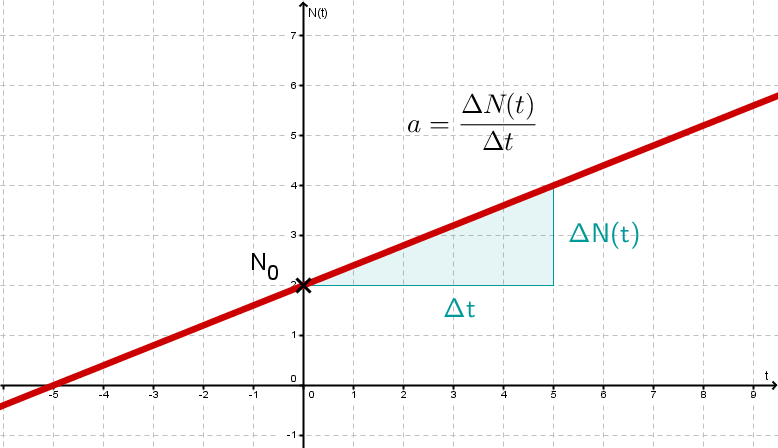
في النمو الخطي تكون سرعة النمو قيمة مطلقة ثابتة. وهذه هى ابسط صور النمو واسهلها. مثال على ذلك سيارة تتحرك بسرعة منتظمة 100 كم في الساعة. ففى كل ساعة تزيد المسافة 100 كم. ومثال اخر هو مبارايات كرة القدم. حيث كلما فاز فريق في مباراة حصل على ثلاث نقاط. لا يوجد فرق بين فريق واخر ولا يشذ احد عن تلك القاعدة. واذا اردنا ان نصيغ هذا فى صورة رياضية فتكون هذا الصورة:
B’(t) = k
حيث ان B يرمز الى الكمية المتغيرة اللتى ندرسها. والشرطة فوق ال B تعنى اننا هنا ندرس سرعة تغير B و k هو ثابت ما. وترمز t الى الزمن. اى اننا نقول ان سرعة تغير الكمية هى دائما قيمة ثابتة. ومن يدرون بالتكامل يعلمون ان اجراء عملية التكامل لهذه الدالة هو امر سهل وان صورة التكامل النهائية هى
B(t) = k.t +c
حيث c هى ثابت أخر. وهذه معادلة خط مستقيم. نرى صورته فى الرسم في الأسفل . ومن هنا حصل هذا النوع من النمو على اسمه.
بيد اننا نعلم ان جائحة الكورونا لا تنتشر وفقا لهذا النمط وياليتها كانت كذلك. فالزيادة فى الاصابات ليست قيمة ثابتة يوميا. ولكن كما نعلم من وسائل الانباء انها رقم متغير. وتكون الطامة الكبري عندما يكون هذا التغير اليومي فى تسارع شديد.
النمو الاسى
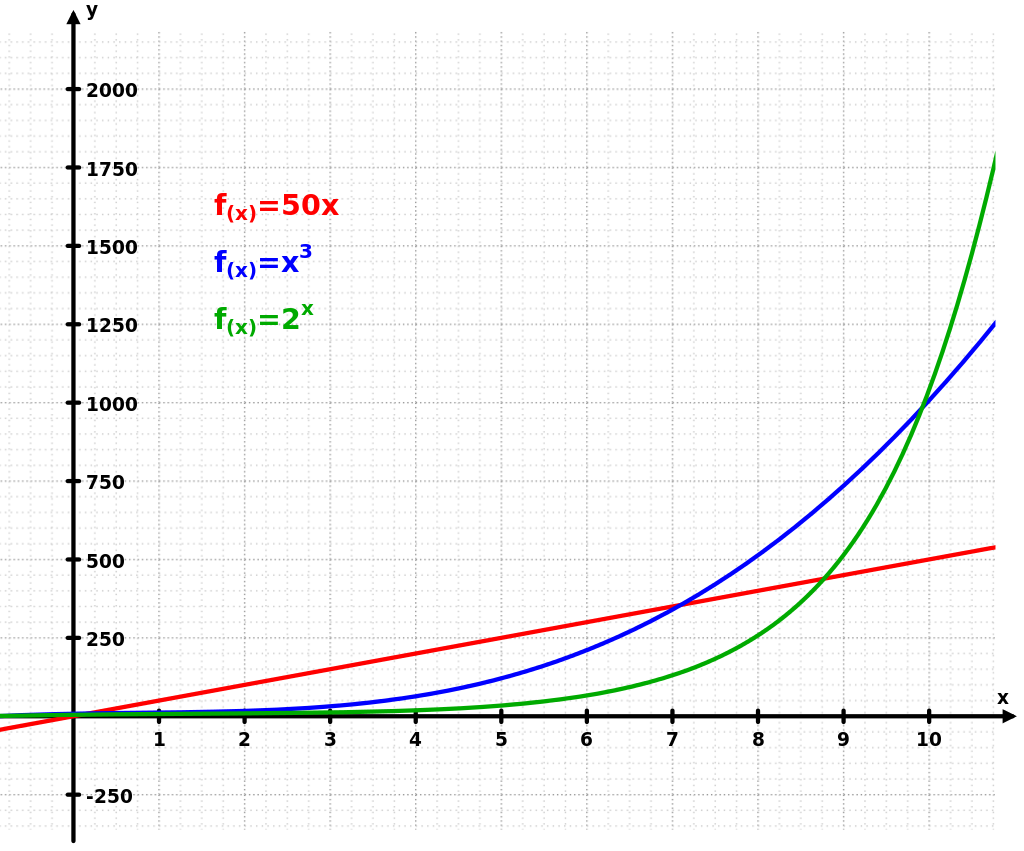
النوع الثاني من النمو هو النمو الاسي. وهنا لا تكون الزيادة فى وحدة الزمن رقما ثابتا مطلقا كما هو الحال في النمو الخطي. ولكن يكون معدل النمو في اضطراد وفى تزايد مستمر يتناسب مع الكمية الموجودة نفسها. واعطي مثالا لهذ النوع سيارة تزداد سرعتها كلما اوغلت فى المسافة فتصبح اعلى من سرعة الطائرة واسرع من الصاروح بل او أسرع من الضوء نفسه لوجاز لها ذلك ولكن طبعا لن يجوز. مثالا اخر هو نظام خاص لتنظيم مبارايات كرة القدم يحابى الاقوياء. حيث لا يحصل كل الفائزون بعد كل مباراة يفوزون بها على ثلاث نقاط . فمثلا عندا يفور برشلونة او ريال مدريد فيحصلون على 6 نقاط بينما اذا فاز فريق فى اخر الجدول يحصل على نقطة واحدة فقط. وهذا النظام يعطى ميزة للاغنياء. مثال اخر اكثر واقعية هو نظام الفائدة فى البنوك. فبعد كل سنة لا يحصل كل المودعون على قيمة نقدية مطلقة ثابتة. فمليونير سوف تزداد امواله بكل تأكيد أكثر من ايداعات شخص كل رصيده فى البنك هو عشرة دولارات فقط. صحيح ان كلهم يحصلون على نفس النسبة. ولكنها نسبة من أصل المال. وهو مختلف فى كل حالة. ومرة اخرى اذا اردنا صياغة ذلك فى صورة رياضية سنحصل على الصورة التالية
B’(t)=k.B(t)
وعندما نكامل تلك المعادلة سوف نحصل على الصورة التالية
B(t) = A.e^(k.t)
حيث مرة اخرى k هو ثابت وe هو الثابت النايبيري وA هي القيمة الابتدائية. واذا رسمنا تلك المعادلة سوف نحصل علي الصورة التالية.
ونسمع كثيرا ان فيروس كورونا ينتشر فى صورة اسية. ولكن هذا ليس صحيح. فاذا نظرنا الى الصورة سنجد ان سرعة الزيادة دائما فى تسارع وان المقدار النهائى يطمح ان يصل الى مالانهاية. ولكننا نعلم فى موضوع نمو الفيروسات ان هذا غير ممكن وغير صحيح وان النمو لا يمكن ان يستمر الى مالانهاية. وان هناك حد ما لهذه الزيادة وهذا النمو.
النمو المحصور
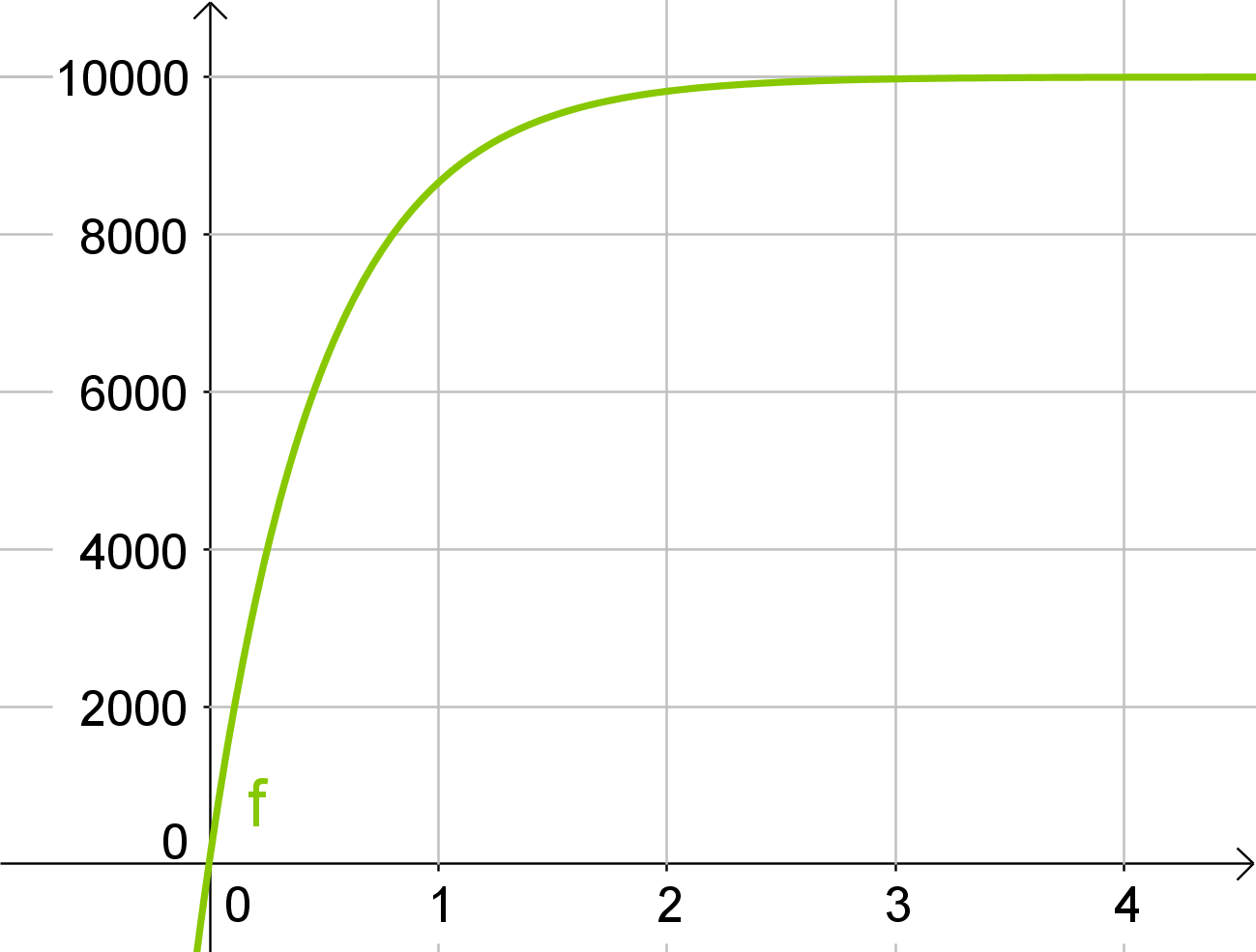
وهذا النوع من النمو هو عكس النوع السابق. حيث انه يحابي الفقراء. ويوجد في هذا النوع من النمو سقف لايمكن للقيمة النهائية ان تتخطاه. وتكون سرعة النمو اكبر مايمكن فى البداية عندما يكون الفارق كبيرا بين القيمة الابتدائية وذلك السقف. ثم تأخذ تلك السرعة تقل بشدة كلما اقتربنا الى هدفنا. مثال على ذلك سيارة تنطلق بأقصى سرعة فى البداية وتقل سرعتها حتى تصل صفرا حينما تصل الى هدفها. ومثال اخر هو نظام لدوريات كرة القدم عندما يفوز فيه فريق فى اخر الترتيب يحصل على 6 نقاط بينما اذا فاز فريق فى المقدمة حصل على نقطة واحدة فقط. واذا اردنا ان نعبر عن هذا بصورة رياضية فستكون الصورة التالية:
B’(t) = k.(S-B(t))
حيث ترمز S هنا الى ذلك السقف اللذى ذكرناه سابقا. ونجد ان سرعة التغير تتناسب مع الفرق بين السقف والقيمة الحالية. فكلما كان الفرق كبيرا كلما كانت سرعة الزيادة أعلى. واذا اردنا اعطاء مثالا واقعيا فهو افتتاح متجر جديد فى مدينة تعداد سكانها 20 الف مثلا. ففى البداية يكون اقبال العملاء الجدد على المتجر شديدا. ولكن هناك حد اقصى لكل العملاء الممكنين وهو عدد سكان المدينة او ال عشرون الفا. وكلما اقترب عدد العملاء من هذه القيمة قلت سرعة زيادة اكتساب العملاء الجدد. لكننا نلاحظ ان هذا النوع من النمو لا يتناسب تماما مع انتشار فيروس الكورونا. حيث لا تكون سرعة انتشار الفيروس في البداية هى أعلى ما يمكن ثم تنخفض تلك القيمة باستمرار. بل على العكس ففى البداية تكون سرعة الزيادة قليلة ثم انها بعد ذلك تزداد.
النمو اللوجستي
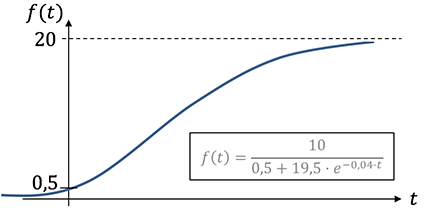
وهذا النوع من النمو يحتوي علي سمات النوعين السابقين. حيث تتناسب سرعة الزيادة مع القيمة الموجود ومع النقص عن سقف معين فى نفس الوقت. فتكون النتيجة انها تحابي الموجودين في الوسط!! حيث ان في البداية يكون النقص كبيرا ولكن تكون القيمة المتوفرة قليلة فتكون سرعة التغير قليلة وعند النهاية تزداد القيمة ولكن يكون النقص قليلا فمرة اخري تكون سرعة الزيادة قليلة. لكن فى المنتصف تكون كلا من القيمة الانية والنقص الاني قيما معتبرة فتكون سرعة التغير اكبر ما يمكن. ويمكن ان نعبر عن ذلك رياضيا بالصورة التالية:
B’(t) = k.(S-B(t)).B(t)
واذا اسقطنا هذا النمو على مثال السيارة فتكون سرعة السيارة قليلة فى البداية تم تزداد شيئا فشيئ حتى تصبح أعلى ما يمكن فى منتصف المسافة. ثم تبدأ السرعة فى التناقص حتى تصل صفرا حين تصل الى هدفها. واذا اسقطنا هذا النوع من النمو على مثال تنظيم دوريات كرة القدم نجد ان الفرق الفائزة والموجودة فى منتصف الترتيب تحصل على نقاط اعلى من الفرق الموجودة فى اول الترتيب أواخره. وهذا النوع من النمو هو الاكثر وصفا لانتشار فيروس كورونا. حيث تكون البداية بسرعة قليلة ثم تزداد السرعة بشدة حتى تصل الى نقطة الانقلاب اللتى تبدأ سرعة الانتشار بعدها في النزول حتى تصل قيمة الاصابات الى سقفها اللذى لايمكن ان يكون الى مالانهاية. فانتشار الفيروس مرتبط بالنهاية بسكان مدينة معينة او دولة معينة اوبحد اقصى هو عدد سكان الكرة الأرضية
واجراء عملية التكامل للدالة السابقة امرا ليس صعبا وليس سهلا. ولكني لن اتعرض لفنياته وسأعطى فقط القيمة النهائية وهي
B(t)= A.S/(A+(S-A).e^(-S.k.t))
وصورة تلك الدالى تكون على شكل حرف S فى اللغة الأنجليزية وهى موجودة فى الصورة التالية فى الأسفل
دعونا نرى كيف يمكننا ان نطبق ذلك عملية على انتشار جائحة الكورونا وهنا سوف افترض الامور التالية:
سوف افترض ان هناك نسبة ثابتة بين حالات الاصابة وحالات الوفيات. اما الدافع الى ذلك فهو الى صعوبة تحديد عدد الاصابات بدقة. فمعظم بل وكل دول العالم لا تستطيع ان ترصد كل حالات الاصابة. بل ان هناك من يقولون ان دولة مثل المانيا واللتى هى من افضل دول العالم في رصد حالات الاصابة ان لم تكن افضلها ان عدد الاصابات فيها هو عشرة اضعاف الرقم المقاس فعليا. والسبب فى ذلك ان حوالى 30% من المصابين لا تظهر عليهم اي اعراض واكثر من 55% تظهر عليهم اعراض بسيطة فقط. كما ان اختبارات الرصد مكلفة الى حد ما وغير متوفرة بالشكل الكافى اللذي يسمح بتسجيل كل الحالات الموجودة. وربما تكون النسبة بين عدد الوفيات الى عدد الاصابات هى واحد الى الف تقريبا. فاذا كانت هناك عشر حالات وفاة فان ذلك يعنى وجود عشرة الاف اصابة تقريبا. وذلك بسبب ان حالات الوفاة تتأخر عن حالة الاصابة ب عشرين يوما في المتوسط تنشأ فيها اصابات جديدة. فاذا انقشعت ازمة الكورونا سنجد ان نسبة الوفيات الى الاصابات الكلية ربما تكون واحد بالمائة.
الأفتراض الثانى ان سرعة انتشار الفيروس تعتمد على عدد المصابين اللذين هم مصدر العدوى الوحيد. لان هذا المرض لا ينتقل الا من بشر الى بشر. كما انها تعتمد ايضا على عدد غير المصابين الموجودين واللذين يمكن ان تنتقل العدوى اليهم كانتشار النار في الهشيم. وباقى العوامل الاخري تتجسد فى صورة الثابت k وساتجاهلها تماما وهذه العوامل قد تكون مرتبطة بمجهودات الدول للكبح من انتشار الفيروس واجراءات العزل. كما انها قد تتعلق بتغير درجات الحرارة والدخول الى فصل الصيف او الشتاء
وسأفترض ايضا ان نقطة الانقلاب ستكون عندما تبلغ سرعة انتشار المرض مداها. بعدها سيأخذ ذلك المرض فى الانحسار. وقد قمت بعمل برنامج يحاكي تطبيق هذا النوع من النمو على الدول المختلفة ويمكنكم ان تروا النتيجة هنا فى هذا الرابط
https://eltawil.org/corona_modelling/logistic_function/index.php