لم يسلم كتاب العناصر لاقليدس من انتقادات الرياضيين القدماء والمعاصرين. ولم يكن محتوى الكتاب هو موضع التثريب و النقد. ولكنها صياغته!  وما الرياضيات الا الصياغة! هى فى ذلك تشبه القانون اللذى يجب ان تكون صياغته دقيقة ومنضبطة بحيث لا يتولد عند من يقرأه اى لبس وبحيث يستطيع المتعاملون معاه استنباط الأحكام من نصوصه اللتى ينبغي ان تكون سليمة فى صياغتها واضحة فى دلالتها غير متناقضة فيما بينها.

وموضوع اليوم ربما يكون جاف ومتقدم وتناولنا له سيكون بشكل سريع غير مفصل. لكنه مع ذلك سيمكننا من القيام برحلة فى بساتين مختلفة نسيح خلالها فى حدائق الرياضيات و الادب و النحو و التاريخ و اللغات!

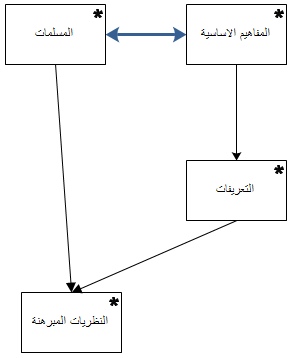
لكن لماذا انتقد الرياضيون كتاب العناصر؟ نعلم ان الاساس اللذى بنى فوقه كتاب العناصر يتكون من 23 تعريفا و 5 بديهيات و 5 مسلمات لن نسردها هنا بالتفصيل لكن لمن يرغب فى مراجعتها سيجدها موجودة فى هذا الرابط. ونستطيع ان نلخص الانتقادات الموجهة الى كتاب العناصر في 3 عناوين رئيسة:

الاعتراض الأول هو الاسلوب اللغوي. فبعض صياغات الكتاب مبهمة وغير موفقة. مثلا التعريف الرابع يقول: المستقيم هو خط يتطابق مع مع استواء النقاط اللتى تقع فوقه. فماذا يعنى استواء النقاط؟ والبعض اعترض ان هناك صياغات افضل. مثلا بروكليوس Proclus  اللذي عاش فى القرن الخامس الميلادي اعترض على التعريف الثاني اللذي يقول: الخط هو طول بلا عرض. وقال بل ان: الخط هو مسار نقطة تتحرك. لكن وكما نلمس فأن هذه الاعتراضات ليس عميقة بل وربما تعود احيانا الى أختلاف الاذواق وحلها سهل وهو اعادة صياعة التعريفات و البديهيات باسلوب اخر.

اما الاعتراض الثانى فهو ان التعريفات و المسلمات والبديهيات ليست كاملة. فنجد اقليدس يتحدث فجأء عن التطابق وهو لم يمهد له مسبقا. وهناك اعتراضات كثيرة قديمة وحديثة حول براهين الانشاء وازاحة الاجسام الجاسئة اللتي لا يوجد لها اى ذكر فى الجزء التأسيسى من الكتاب. وحل هذا الاعتراض هو استكمال لائحة التعريفات والمسلمات والبديهيات حتى تشمل كل العناصر اللازمة لصياغة كل التعبيرات الهندسية مع القدرة على برهانتها او ضحضها.

ثم نصل الى الاعتراض الاقوى والأهم بالنسبة لنا اليوم. وهو ان صياغة تعريفات ومسلمات وبديهيات اقليدس تحتوى على خلل واضح. مثلا التعريف الاول يقول : النقطة هى مالا جزء له. لكن ما هو الجزء؟ فالتعاريف نفسها قائمة على مصطلحات غير معرفة! وقائمة المفاهيم المستخدمة الغير معرفة طويلة مثل: نهاية وعرض وطول الى اخره. فكأننا نسير فى طريق يأخذنا الى طريق اخر حتى نصل فى النهاية الى طريق مسدود. وكأن عمارتنا متينة الطوابق نكتشف فجأة ان طابقها الأول لم يتم تاسيسه! فقد يكون واقفا فوق صخر او طبقات متحللة او قنابل موقوتة! والسؤال الان ماهى الطريقة السحرية اللتى ينبغى ان نصيغ الهندسة بها حتى لا نصل الى طريق مسدود ونؤسس لكل المكونات اللتى نستخدمها حتى لوكانت اللبنة الاولى؟!

وقبل ان نشرع فى تقديم ذلك الحل السحرى وتوضيح الصياغة المعاصرة للهندسة دعونا نستعرض اولا ماهى الشروط المطلوب توافرها فى أي صياغة معاصرة؟ يجب طبعا ان تتلافى الانتقادات السابقة بالاضافة الى امور اخرى. فيجب للصياغة  ان تكون:

1 واضحة لاينشأ اي لبس لدى من يقرأها كنص قانونى سليم.
2 ان تكون مسلماتها كاملة تعطينا القدرة على صياغة أي تعبير هندسي مع القدرة على برهنته او نفيه
3 ان تؤسس لكل مفاهيمها ولا تتركها معلقة فى الهواء حتى لوكانت المفاهيم الاولي
4 الا تكون مسلماتها متناقضة فيما بينها. بحيث يستحيل ان تتحقق كلها فى نفس الوقت. تماما كما لا يجوز تشريع قوانين متناقضة.
5 ان تكون مسلماتها بليغة كنص ادبى رفيع. ومعنى البلاغة ان يكون شعارها ما قل ودل وأن توجز فتنجز. فالمطلوب هو استخدام اقل عدد من المسلمات للوصول الى افضل نتيجة. لذلك يجب ان تكون المسلمات مستقلة عن بعضها لا يمكن ان نبرهن احدها بدلالة الاخريات. واذا حدث ذلك فعلينا ان نحذف هذه المسلمة الغير مستقلة من لائحة المسلمات ونتعامل معها كنتيجة او نظرية.
6 ان تكون لمسلماتها علاقة بالواقع ولا تكون مجرد شطح بالخيال فى مواضيع لا قيمة لها. وهذا الشرط هو اضعف الشروط. فكيف لنا ان نحددا مسبقا ما هو شطح بالخيال وما هو واقعى؟ فسابقا ظن الناس ان الهندسات الغير اقليدية شطح بالخيال لافائدة من وارئه ثم تبين لهم بعد ذلك لاحقا ان لهذه الهندسة قيمة تطبيقية مهمة جدا.

كان دافد هلبرت David Hilbert الرياضى الألمانى اللذي عاش فى الفترة بين 23 يناير 1862 حتى 14 فبراير 1943ميلادية هو أول من قدم صياغة رياضية سليمة للهندسة الاقليدية. ولكنه لم يكن الوحيد ولا الأخير. فهناك العديد من الصياغات الاخرى اللتى تختلف فيما بينها فى الكثير او القليل. وفي حين ان صياغة هلبرت ليست الاكثر سهولة الا أنها الأكثر اناقة وبلاغة فهى تتطلب اقل عدد من المسلمات. واليوم سنتعرض لصياغة اخرى لاقليدس القرن العشرين: الرياضى الروسى اندريه كولموغوروف Andrei Klomogorow اللذي عاش فى  الفترة بين 25 ابريل 1903 حتى 20 اكتوبر 1987 وذلك بسبب ان صياغته اسهل من صياغة هلبرت من ناحية استنباط النظريات منها!

الخطوة الأولى اللتى خطتها الصياغة المعاصرة هى انها تخلت عن البديهيات. او بمعنى ادق أنها لم تعد تفرق بين البديهيات والمسلمات. ففى حين أن اقليدس قال ان البديهيات هي امور واضحة بالسليقة لانحتاج الى برهنة صحتها وهي شديدة العمومية بينما المسلمات هى ايضا امور واضحة بالسليقة ولكنها ليست عامة بل متخصصة تتعلق بالهندسة ذاتها. ترى الصياغات الحديثة انه طالما كانت التعبيرات البديهية لا تنتمى الى الهندسة فلا يهمنا امرها. ولذلك اسقطت البديهيات من حساباتها تماما وابقت على المسلمات. ولكن اللخبطة الحاصلة ان الصياغة الحديثة تعتبر مصطلحى: “مسلمات” و”بديهيات” مترادفين فاحيانا نجد تلك الكلمة واحيانا نجد الاخرى.

انا شخصيا فافضل مصطلح “مسلمات”. وذلك لسببين. السبب الاول هو الايحاء اللغوي. فالبديهيات مشتقة من البديهة. ونعلم ان الرياضيات مجردة لا تتعلق بالبديهة. وكما قال اينشتاين فان مفاهيم الرياضيات لامعنى منظور لها. اما السبب الثانى فان هناك خطأ من البداية فى ترجة كلمة axiom الى “بديهة” و postulate الي “مسلمة” كما سنرى لاحقا.

الخطوة الثانية وهى الأهم تتعلق بالسؤال الاساس كيف يمكن ان نصيغ  الهندسة حتى تكون كل لبناتها -حتى اللبنة الأولى- مؤسس لها ولا تكون معلقة فى الهواء؟ الأجابة: لذلك نستخدم النحو ونظرية المجموعات ونظرية الأعداد الحقيقية!

فى اللغة العربية يوجد نوعان من الجمل: جملة خبرية وجملة انشائية. اما الجملة الخبرية فهى تحتمل الصدق أو الكذب لذاتها. كأن اقول: طوكيو عاصمة اليابان. هذه جملة قد تكون صحيحة او خاطئة. صادقة او كاذبة. اما الجمل  الانشائية فلا يجوز ان اصف قائلها بانه كاذب او صادق. مثلا السؤال: كم الساعة الأن؟. او الطلب والأمر ك: أقبل الأمر الواقع!

طبعا قواعد اللغات الاجنبية لا تشبه النحو العربى. لكن فكرة الصياغة الحديثة تشبه الجملة الانشائية فى اللغة العربية. فهي تستخدم اسلوبا لا يحتمل الصدق او الكذب. وهنا نرى لماذا أني افضل مصطلح مسلمة Postulate. فالترجمة الحرفية لكلمة Postulate اليونانية هي “طلب“. والترجمة الحرفية ل axiom هى “احتياج“.

فكأن لسان حال الصياغة الحديثة يقول:   أعطنى -يوجد- نقطة ومستقيم ومسافة بحيث يكون التالي:
1 المستقيم هو مجموعة من النقاط
2 لكل نقطتين مختلفتين يوجد مستقيم واحد يحتوى هاتين النقطتين
3 كل مستقيم يحتوى على نقطة واحدة على الأقل
4 توجد على الأقل ثلاث نقط لا تنتمى الى مستقيم.

وقبل ان نسرد باقى المسلمات ينبغى ان نلاحظ التالي:  لابد ان نحدد اولا ما هى المفاهيم الاساسية اللتى نحتاجها لصياغة الهندسة. وفى حالتنا اليوم فأن المفاهيم الاساسية اللتى نحتاجها هى: “النقطة” و”المستقيم” و”المسافة”. وهذه المفاهيم الاساسيسة ليست اشياء مقدسة. ففى حالة صياغة هلبرت نجد ان المفاهيم الاساسية هى: “النقطة” و “المستقيم” و “التطابق”  و”يقع على” و “يقع بين”. كما ان هناك بعض الصياغات لاتعتبر المسافة مفهوما اساسيا وتستبدله بالأزاحة او بالتطابق.

وهذه المفاهيم الاساسية نطلب اولا قبولها من المتلقى طلبا. وكما ان الشعر مبنى على بحور وأوزان فان الصياغة الرياضية  قائمة على تركيب “بما أن    اذن”.  اى أن صحة ما يأتى بعد “اذن” مشروط بتحقق ب “بما ان” اولا!  فنتائج الرياضيات ليست صحيحة فى المطلق وليست مخرجاتها صحيحة الا بعد تحقق مدخلاتها أولا. ونظريات الهندسة لا نضمنها الا بعد ان يعطينا المتلقى قبوله بالمفاهيم الأساسية والمسلمات!

اما هذه المفاهيم الاساسية فهي لامعنى لها الا من خلال المسلمات اللتى توضحها. ويحب ان ننسى كل تلك الرسوم اللتى عرفناها خلال حصص الهندسة حول الخط المستقيم و المثلث الى اخره. فهذه كلها اشياء لا قيمة رياضية لها ولا تدخل فى البرهان. وهي فى أفضل الاحوال نماذج ممكنة ولكنها ليست الهندسة الحقيقية. كما يجب ان ننسى ايضا ما توحيه لنا البديهة او ما نعرفه من اللغة عن تلك الكلمات. فبامكاننا صياغة ما سبق كالتالي: أعطني نبيل وقاسم وسالم بحيث يكون :
1 قاسم مجموعة من نبيل
2 لكل نبيلين مختلفتين يوجد قاسم واحد يحتوى هاذين النبيلين
3 كل قاسم يحتوى على نبيل واحد على الاقل
4 يوجد على الاقل ثلاثة نبيل لاينتمون الى قاسم!
وذلك بدون أى فارق فى المعني

ونلاحظ أستخدام بعض التعبيرات ك: “مجموعة” و “يحتوي” و “يوجد” و”ينتمي“. وهذه كلها تعبيرات خاصة لها معناها الصارم بداخل نظرية المجموعات! وهناك كتابة ورموز خاصة بنظرية المجموعات ولكنى ساتخلى عنها وسأكتب بالكلمات العادية.

وأخيرا علينا ان ننتبه أن الرياضيين يصنفون المسلمات تحت مجموعات مختلفة ليتمكنوا من دراسة خواص كل مجموعة من المسلمات على حدة. والمسلمات الاربعة السابقة تنتمى الى مجموعة “الوقوع على” لكن هنا 4 مجموعات اخرى وهي: “المسافة” و “الانتظام” و “الأزاحة و التطابق” واخير “التوازي“.

مسلمات المسافة:

5 المسافة هي رقم حقيقى غير سالب ننسبه لأي نقطتين. وتكون المسافة بالنسبة لنقطة ونفسها صفر. واذا كان عندنا نقطتان A و B فاننا نرمز للمسافة بينهما ب |AB|
6 المسافة بين A و B تساوى المسافة بين B و A أي أن |AB| = |BA|
7 لاى ثلاث نقاط A و B و C d يكون:
|AB| + |BC| >= |AC|
واذا كانت الثلاث النقاط السابقة تنتمى الى نفس المستقيم. فلابد ان تتحقق احد العلاقات الثلاثة التالية
|AB| + |BC| = |AC|
|AC| + |CB| = |AB|
|BA| + |AC| = |BC|
والعكس صحيح

اذن مااللذى تريد ان تقوله الثلاث مسلمات السابقة؟ انها تقول ان هناك كمية اسمها المسافة تعبر عن العلاقة بين أي نقطتين. وبحيث تكون المسافة بين النقطة ونفسها صفر. وبحيث يكون “طول” اى ضلع فى مثلث اصغر من مجموع الضلعين الأخرين! مع ملاحظة ان تعبير “طول” جديد سأتجاوز واعتبره يساوى مفهوم “المسافة“. وان كان هذا الفرض خاطئا لأن الطول له تعريف اخر فى الهندسة المسلماتية ولكنى لن اذكره هنا!

ما يلفت نظرنا ايضا ان المسلمة السابعة تعطى حلا صياغيا سليما لما عجز عنه اقليدس حينما عرف الخط المسقيم بانه مستوي! فالمسلمة السابعة تعرف الخط المستقيم بانه مجموعة النقاط اللتى تحقق الشرط أن اى 3 نقاط ينتمون اليه تكون المسافة بين نقطتين معينتين منهما تساوي مجوع المسافتين بين هاتين النقطتين والنقطة الثالثة المتبقية!

ثم نصل الى مكون جديد من مكونات الصياغة العصرية وهو “التعريف“. ففى حين اننا عرفنا المفاهيم الاساسية وعلمنا ان ما يحددها بدقة هي المسلمات. فاننا نستطيع ان نشتق من المفاهيم الاساسية تعاريف جديدة. وهى عبارة عن المفاهيم الاساسية  مضافا اليها بعض الشروط. ومثالا للتعاريف فى صياغة كولموغوروف نذكر: “يقع بين” و “القطعة المستقيمة” و”الشعاع” و “الحركة” و “الزاوية” الى اخره. ومرة اخرى نشير الى ان هذه التعريفات ليست اشياء مقدسة. ففى بعض الصياغات الاخرى نجد مثلا ان التطابق ليس تعريفا ولكنه مفهوم اساسى ويتم تحويل احد المفاهيم الاساسية فى المقابل الى تعريف.

وعلى سبيل المثال اعطى كيفية صياغة تعريف “يقع بين“:
نقول ان النقطة B تقع بين A و C عندما يتحقق الشرط التالي: |AC| =|AB| + |BC|

ومن الممتع ان نري كيف تقدم الصياغة الحديثة تعريفا للزاوية بدون تقديم اى رسوم لها! واستكمالا للموضوع  اعطى باقى المسلمات بدون التعليق عليها.

مسلمات الأنتظام

8 لأي شعاع يبدأ من النقطة O ولأي رقم غير سالب a توجد نقطة وحيدة A بحيث يكون a= |OA| a
9 أى مستقيم يقسم المستوى الى مجموعتين من النقاط بحيث تكون القطعة المستقيمة الواصلة بين نقطتين من نفس المجموعة لا تقطع ذلك المستقيم بينما القطعة المستقيمة الواصلة بين نقطتين من مجموعتين مختلفتين لابد وان تقطعه.

مسلمات الازاحة

10 اذا كانت المسافة بين النقطتين A و B ليست صفر وتساوي المسافة بين النقطتين C و D فان هناك ازاحتين ممكنتين لجعل A تنطبق على C و B تنطبق على D وفى خلال هاتين الازاحتين ترتبط كل نقطة من نقاط نصف المستوي بالنسبة للمستقيم AB بنقطة من نقاط نصف المستوي بالنسبة للمستقيم CD

مسلمات التوازي

11 اذا كان لدينا مستقيم ونقطة لا تنتمى اليه فان هناك بحد اقصى مستقيم واحد يحتوى تلك النقطة ويكون موازيا للمستقيم الأول