ما يميز الفيزياء انها تطبيق لبعض القواعد البسيطة على ظواهر طبييعة مختلفة. فتستطيع الفيزياء ان تصف سلوك هذه الظواهر بمنتهى الدقة على الرغم من ان هذه الظواهر قد تكون مختلفة جدا فى مظهرها بل و تبدو وكأنها لا يربطها أى رابط. وتشكل قوانين نيوتن الثلاثة بالأضافة الى قانون الجاذبية لنيوتن القواعد الأساسية للميكانيكا الكلاسيكية.
دعونا اليوم نتعرف على المثال المبسط التالي: دعونا نتخيل رياح تهب افقية تماما على شاطئ فاننا قد نشاهد بعض حبات الرمل الناعمة تتصاعد الى أعلى بالرغم من عدم وجود أى قوى رأسية! فما هو السر فى ذلك؟ انه تأثير برنولى!.
بداية فان برنولى اللذى نعنيه اليوم هو السويسرى دانيال برنولى اللذى ينتمى الى عائلة برنولى الشهيرة فى ميدان العلوم. فهو ابن يوهان برنولى العالم المثير للغط كما ان ياكوب برنولى هو عمه. وكذلك فان لدانيال أخ رياضى يدعى نيكولاوس.
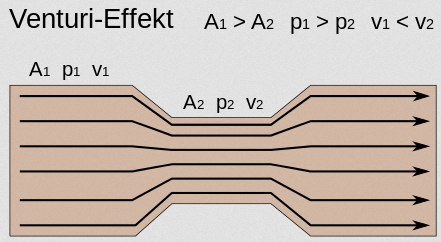
وقبل ان نستفيض فى تأثير برنولى دعونا نرى ظاهرة اخرى ممهدة وهى ظاهرة فنتورى. وهذه الظاهرة تقول ان الموائع الغير قابلة للانضغاط كالماء مثلا تزداد سرعة مرورها فى مقطع اذا كان ضيقا بينما تقل سرعة سريانها اذا كان المقطع واسعا. وهذه الظاهرة نعرفها جيدا عندما نضغط على فتحة خرطوم يسرى فيه الماء فسوف نشاهد اندفاع سيلان الماء بسرعة اعلى. واذا تدفق الماء فى انبوبة ذات مقاطع مختلفة المساحة عبر طولها فلكى تبقى كمية الماء المتدفقة ثابتة وحيث ان الماء هو مادة غير قابلة للأنضغاط فتكون سرعة الماء فى المقاطع الضيقة اسرع منها فى المقاطع الواسعة.
وهنا يظهر سؤال: حيث ان كتلة الماء المتدفقة فى وحدة الزمن ثابتة وحيث ان سرعة الماء فى المقاطع الضيقة عالية. اذن فلابد أن ترتفع طاقة حركة الماء فى المقاطع الضيقة عنها فى المقاطع العريضة. لكن كيف يمكن تبرير ارتفاع قيمة طاقة الحركة فى المقاطع الضيقة ونحن نعلم ان الطاقة لا تفنى أو تستحدث من العدم؟
وهنا يأتى مبدأ برنولى ليفسر هذا الأمر ويقول انه عندما ترتفع السرعة فان الضغط يقل. وبالتالي فكما ترتفع طاقة الحركة فان طاقة الوضع تقل وبحيث يصبح المجموع الكلى للطاقات ثابتا! فيقول قانون برنولى
v^2/2 + p/d= constant
حيث v هي السرعة و p الضغط و d الكثافة. ونلاحظ من القانون انه كلما زادت السرعة قل الضغط وبالعكس.
ويمكن برهنة هذا القانون بسهولة من القانون الثانى لنيوتن. لكن البرهان الرياضى لن يهمنا اليوم. فما يهمنا هو تطبيقات هذا القانون فى الحياة.
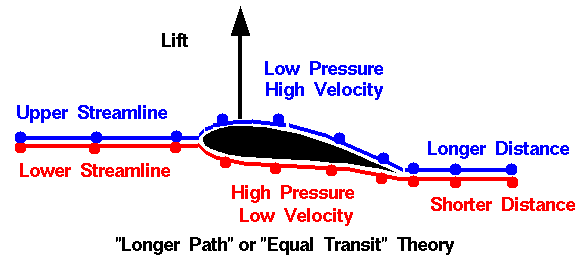
اول تطبيق لتأثير برنولى يمكننا أن نلمسه فى ميدان الطيران. حيث يشكل مبدأ برنولى العامل الرئيس اللذى يرفع الطائرات الى اعلى. فعندما تندفع الطائرات الى الأمام ينساب الهواء فوق وأسفل جناح الطائرة. وبسبب شكل جناح الطائرة المميز فان الهواء يسلك فوق جناح الطائرة مسارا أطول منه اسفل الجناح. وحيث ان الهواء غير قابل للأنضغاط فلابد ان تكون سرعة الهواء أعلى الجناح اقل منها اسفل الجناح. وبالتالى يكون الضغط اسفل الجناح اعلى منه أعلى الجناح فترتفع الطائرة الى أعلى. وما يهمنا هنا هى السرعة النسبية بين جناح الطائرة و الهواء وليست الحركة المطلقة. فمثلا أن هبت رياح عاصفة فوق طائرات خفيقة رابضة فوق الأرض فانها ان لم تكن مشدودة الى الارض بسلاسل فسوف ترتفع فى الهواء.
وهنا نعود مرة اخرى الى السؤال المطروح فى أول الموضوع والمتعلق بارتفاع حبات الرمل الى أعلى. فعندما تهب الرياح وبسبب شكل حبة الرمل تكون سرعة الهواء اعلى حبة الرمل اقل منها اسفلها فيتفوق الضغط فى اسفلها فترتفع حبة الرمل الى اعلى.
اذن بالرغم من الاختلاف الظاهرى بين سريان الماء فى انبوب مختلف القطر وتحليق طائرة فى الجو وارتفاع حبة رمل فى الهواء فان المبدأ الاساس واحد. بل يوجد لتأثير برنولى تطبيقات اكثر غرابة. فبسبب هذا المبدأ لا ينبغى ان نقترب من القطارات السريعة بصورة أكثر من اللازم. لان سرعة الهوء بين القطار وجسمنا تكون اعلى من سرعة الهواء خلف ظهورنا فيكن الضغط خلف ظهورنا اعلى من الضغط امامنا مما يدفعنا باتجاه القطار المندفع من الامام ومما قد يعرض حياتنا للخطر.
بل هناك تطبيق غريب لمبدأ برنولى نلمسه فى ميدان كرة القدم. فلاعبو كرة القدم يركلون الكرة بحرفية معينة وبحيث تأخذ مسار مقوسا ملولبا. لكن كيف يتم هذا؟ هذا يتم عبر مبدأ برنولى حيث يتم ركل الكرة الى الامام بطريقة تجعلها تتحرك الى الأمام و تدور حول محورها فى نفس الوقت. اذن تكون سرعة الهواء عند نقاط على سطحها اعلى منها من النقاط المقابلة لها على امتداد القطر مما يجعل الكرة تأخذ مسارا ملتويا


كيف يمكن للهواء ان يكون غير قابل للانضغاط ؟!
العبارة ليست مطلقة. ولكنها نسبية. فالهواء طبعا قابل للأنضغاط ولكن لابد من بذل جهد خارجي حتى نضغط الهواء وكلما ازدادت كثافة الهوء كلما زاد الأمر صعوبة
وحيث ان الهواء غير قابل للأنضغاط فلابد ان تكون سرعة الهواء أعلى الجناح اقل منها اسفل الجناح…. اخي اعتقد ان الامر معكوس فالسرعة اعلى الجناح اكبر منها اسفل الجتاح… و نفس الملاحظة في “حبة الرمل تكون سرعة الهواء اعلى حبة الرمل اقل منها اسفلها فيتفوق الضغط فى اسفلها فترتفع حبة الرمل الى اعلى… مشكور اخي على المجهود، حقيقة معلومات مهمة جدا..
شكرا للتصويب. انت طبعا محق. كان هذا خطأ كتابي. سرعة الهواء اعلى الجناح اعلى منها فى اسفله لانه يقطع مساقة اطول فى نفس الزمن تقريبا. والمثل بالنسبة لحبة الرمل
لتاثير برنولي تطبيق طبي وهو اهتزاز الحبال الصوتية ايضا
فعندما يمر الهواء بين الحبلان الصوتيان ينخفض الضغط بينهما فينطبقان بتاثير برنولي ويرتفع الضغط تحتهما فينفتحان مجددا ويهتزان مولدان الصوت الخام
كما في تجربة النفخ بين ورقتين على عكس المتوقع تنطبقان ايضا