تبدو فكرة الاعداد المركبة وفلسفة وجودها غير بديهية بالنسبة للبعض. لكن على الرغم من ذلك فان التعامل معها حسابيا هو امر سهل و بديهى حتى بالنسبة لهؤلاء اللذين يرون فكرتها الاساسية غير بديهية. فمعظم العمليات الرياضية اللتى نجريها على الاعداد الحقيقية بالامكان اجراؤها على الاعداد المركبة وبصورة مشابهة. فلجمع عددين مركبين مثلا نجد ان العملية تتم هكذا:
(1+2i)+(3+4i)=(4+6i)
اي اننا نجمع الجزء الحقيقى على الجزء الحقيقى والجزء التخيلى على الجزء التخيلى
وعملية الطرح هى العملية العكسية بالنسبة لعملية الجمع وبناء على ذلك نجد الاتى
(4+6i)-(3+4i)=(1+2i)
وبالمثل فعملية ضرب عدد مركب فى عدد مركب هى عملية ممكنة. وهى تشبه عملية ضرب قوسين يحتوى كل قوس على اعداد حقيقية مجموعة على بعضها. وكما نعلم تتم عملية الضرب فى هذه الحالة بان نضرب كل عنصر فى القوس الاول فى كل عنصر موجود فى القوس الثانى ثم نجمع النتائج على بعضها. او كما يتعلم التلاميذ فى المدارس: كل عنصر فى القوس الاول يصافح كل عنصر فى القوس الثانى!!. ومن هنا
(1+2i)*(3+4i)=(3+4i+6i+8i^2)
=(3+10i+8i^2)
واذا راعينا ان i^2 تساوي سالب واحد نحصل على:
(3+10i-8)=(-5+10i)
ونلاحظ هنا ان التعامل الرياضى مع الاعداد المركبة يتشابه الى حد هائل مع التعامل مع الاعداد الحقيقية. وخاصية الضرب الاخيرة تمهد الطريق الى خاصية للاعداد المركبة تعرف بالعدد المكمل . حيث لكل عدد مركب عدد اخر مركب مكمل له بحيث اذا ضربنا العددين فى بعضهما حصلنا على نتيجة حقيقية خالصة دون شق تخيلى. والعدد المكمل يكافيئ تماما العدد الاساسى مع عكس اشارة الشق التخيلى فيه. فمثلا العدد (1+2i) العدد المكمل له هو (1-2i) واذا ضربنا العددين فى بعضهما حصلنا على 5
كما ان للعدد المركب خاصية اخرى تعرف بالقيمة المطلقة وهى تحسب باخذ الجذر التربيعى لمجموع مربعي الشقين الحقيقى و التخيلى . فمثلا القيمة المطلقة للعدد (3+4i) تساوي
sqrt(9+16) =5
كما انه بالامكان حساب الجذر التربيعى للعدد المركب. وهو عبارة عن عدد مركب اخر اذا ضربناه فى نفسه يعطينا قيمة العدد المركب اللذى نبحث عن جذر له. فمثلا الجذر التربيعى ل (3+4i) هو (2+i) ويمكننا التأكد من ذلك بضرب (2+i) فى نفسه ونرى على ماذا سوف نحصل.

هنا ينتهى الجزء الاول من موضوع اليوم. وفى الجزء الثانى سنحاول ان نصنع نوعا جديدا من الجبر. و لا اقول هنا نوعا جديدا من الاعداد بل نوع جديد من الجبر. وهنا قد يبرز سؤال وهل هناك انواع مختلفة من الجبر؟ و الاجابة هى نعم. فمثلا هناك الجبر البوليانى اللذي يستخدم فى صناعة اجهزة الكمبيوتر. ومن الاشياء الغريبة فيه ان جمع واحد زائد واحد يعطى صفرا. وهناك فرع الجبر المجرد اللذى يعنى بدراسة الجبر فى صورته العامة والمطلقة. كما قد يهتم علم مثلا بدراسة خواص الشعر بغض النظر ان كان باللغة العربية او الصينية ويبحث عن اجابة لسؤال وهو : ماهو الشئ اللذى يجعل من الشعر شعرا على الاطلاق؟. وموضوع الجبر المجرد هو موضوع كبير ولا يتسع له المكان هنا. ولكننا سوف نتعرض له فى موضوع اليوم بقدر حاجتنا الى ذلك.

لكى نخترع جبرا جديدا لابد ان يكون لدينا اولا مجموعة اشياء رياضية لنجري حساباتنا عليها. وفى الجزء الاول من موضوعنا اليوم كانت هذه المجموعة هى مجموعة الاعداد المركبة. وفى حال التعامل مع الاعداد الحقيقية تكون المجموعة المستخدمة هى مجموعة الاعداد الحقيفية وهكذا. ولكننا هنا فى جبرنا الجديد لن نستخدم مجموعة اعداد بشكل مباشر. فمجموعتنا اللتى سوف نستخدمها هي مجموعة النقاط الهندسية اللتى تقع فى مستوي افقى!!. فنحن سنستخدم اشياء هندسية فى اجراء عمليات الجبر. ولكننا كما نعلم من جهة اخري ان اى نقطة فى مستوي يمكننا ان نعبر عنها برقمين حقيقيين يمثلان احداثيات هذه النقطة. اى اننا فى النهاية نستخدم مجموعة الاعداد الحقيقية بشكل غير مباشر. والتعبير الرياضى السليم لما نفعله اننا نستخدم مجموعة لها شكل R*R حيث ترمز R هنا الى مجموعة الاعداد الحقيقية. ونلاحظ هنا اننا نتستخدم R مرتين لان كل عدد له احداثيان وليس احداثيا واحد. وعلامة الضرب ترمز الى عملية الضرب الكارتيزي . وهى عملية ضرب مجموعتين فى بعضهما وبناء عليها فان كل عنصر فى المجموعة الاولى يصافح كل عنصر فى المجموعة الثانية. مثلا العملية التالية:
{1,2}*{3,4} = {(1,3),(1,4),(2,3),(2,4)}

ويقول الجبر المجرد ايضا اننا نحتاج فى الجبر الجديد الى عملية رياضية نطلق عليها عملية الجمع. وهنا لا يجب ان نخلط بين عملية الجمع فى هذا السياق وعملية الجمع التقليدية اللتى يتعلمها التلاميذ فى المدارس. فالمقصود بعملية الجمع هنا انها عملية تربط بين عنصرين من المجموعة ويكون الناتج عنصرا من نفس المجموعة. وفى جبرنا الجديد عندما نجمع نقطتين على بعضهما نحصل على نقطة جديدة و نعرف عملية الجمع هكذا.
(1,2)+(3,4) =(4,6)
وعلمية الطرح هي ايضا ممكنة فهي العملية العكسية للجمع. وبناء على ذلك
(4,6)-(3,4)=(1,2)
ويتطلب الجبر المجرد ايضا وجود عملية تسمى عملية الضرب. وهى كما تتوقعون لا علاقة لها ايضا بعملية الضرب اللتى تعلمناها فى المدارس ولكنها عملية ربط جديدة تربط بين عنصرين من المجموعة ويكون الناتج عنصرا يننمى ايضا الى نفس المجموعة. وهنا فى حالتنا سوف نضرب نقطة فى نقطة ونحصل على نقطة جدية. وسوف نعرف عملية الضرب هكذا
(a,b)*(c,d)=(ac-bd,ad+bc)
وبناء عليه فان ضرب النقطتين السابقتن يتم على الشكل التالى:
(1,2)*(3,4)=(5-,10)

وهنا سوف نلاحظ شئ غريب جدا وهو ان النتائج اللتى حصلنا عليها فى الجزء الثانى من موضوع اليوم تتفق تماما مع نتائج الحزء الاول. مع مراعاة اننا فى الجزء الثانى لم نستخدم ابدا اعدادا تخيلية ولكننا كنا نستخدم زوجا من الاعداد الحقيقية. ويقول الرياضيون ان بناء الجبر الجديد اللذى حصلنا عليه يتطابق تماما مع جبر الاعداد المركبة فى صورته الاولى ويقولون ان البناءان متماثلان او isomorph .ويطلق على هذا الجبر الجديد طريقة جاوس للتعبير عن الاعداد المركبة. وهى تعبر عن الاعداد المركبة فى شكل نقاط مرسومة على مستوي افقيى تعبر قيمة الاحداثى السينى عن الشق الحقيقي للعدد المركب بينما يعبر الاحداثى الصادي عن الشق التخيلي منه.

ومن هنا نري ان من يشعر بالضيق من فكرة الاعداد التخيلية و مازال لايستطيع ان يهضمها بامكانه تخيل الاعداد المركبة فى صورة لا تحتوي على اعداد تخيلية نهائيا. ولكن هنا يجب علينا ان نتخيل ان العدد المركب يعيش في بعدين وليس بعد واحد فقط. والبعد التخيلى يمثل دائما بعدا مغايرا للبعد الحقيقى. والشق التخيلى والحقيقى فى العدد المركب بغض النظر عن اسمائهما يمثلان بعدين حقيقيين مختلفين فى عالم الاعداد.

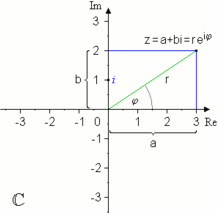
ولكن ليست هذه كل الصور الممكنة للتعبير عن الاعداد المركبة فهناك صورة اخرى يمكن ان تكون اقل شهرة من الصورتين السابقتين ولكنها قد تكون اهم منهما قيمة عمليا. فهذه الصورة تستخدم فى الميادين الهندسية و الرياضية المختلفة. وهى اهم نظرا لانها اقصر طولا واسهل رياضيا فى التعامل معها. وهى تشبه الصورة الثانية من حيث اننا نعبر فيها عن نقطة ما بدلالة احداثياتها. ولكننا لن نستخدم هذه المرة الاحداثيات الكارتيزية ولكن الاحداثيات القطبية. اى تلك الاحداثيات اللتى تحتاج الى بعد النقطة عن نقطة الاصل كما انها تحتاج ايضا الى الزاوية اللتى يصنعها الخط الواصل بين نقطتنا ونقطة الاصل مع المحور الافقى. كما تشبه الصورة الثالثة الجديدة الصورة الاولى من ناحية انها تحتوي على الاعداد التخيلية مرة اخرى. وبناء على هذا فاننا يمكننا ان نعبر عن العدد بهذه الصورة
3+4i = 5e^0.93i

الاعداد المركبة

وحيث ان الابداع الرياضى لا حدود له فان هناك صور رابعة تعبر ايضا عن الاعداد المركبة وهىى مرة اخرى لا تستخدم الاعداد التخيلية ولكن الاعداد الحقيقية فقط. ولكنها تستخدم صورة المصفوفات. فالعدد السابق يمكن التعبير عنه فى الصورة التالية:
3+4i =|3 -4| 1
2 |3 4|
كما ان العمليات الحسابية اللتى يمكن اجراؤها على الاعداد المركبة يمكن اجراؤها هنا بواسطة المصفوقات ثم الوصول طبعا فى النهاية لنفس النتيجة!!!

فى النهابة وبعد ان تعرفنا على صور مختلفة للاعداد المركبة من المفيد ان نذكر ان الاعداد المركبة ليست هى اعلى انواع الاعداد او اوسعها. فهناك اعداد اخري اوسع من الاعداد المركبة وهى اشد تركيبا منها وهذه الاعداد تعرف باسم الكواترنيونات quaterneon وهى تتكون من 4 اعداد او عناصر: عنصر حقيقى و 3 عناصر تخيلية ولكن من انواع مختلفة. كما ان الاعداد الكواترنيونية ليست هى اخر المطاف بل هي مجرد البداية لانواع غير نهائية من الاعداد المركبة تعرف باسم الاعداد المركبة الفائقة hypercomplex number !!

الخلاصة ان الرياضيات ليست قيودا جامدة لا قكاك منها بل هى حرية وابداع لا حدود لها. كما انه من الخطأ ربط الرياضيات بالواقع الفيزيائى ربطا جامد او الخلط بين خواص ظاهرة طبيعية ما وخواص مجموعة الاعداد اللتى يستخدمها نموذج رياضى لتبسيط هذه الظاهرة.