يمكن تقسيم الاعتراضات اللتى واجهت قبول الصفر فى الماضى الى قسمين: اعتراضات فلسفية و اعتراضات رياضية. فاما الاعتراضات الفلسفية فلم تكن موضوعية و كانت خاصة بالاغريق وحدهم. فالاغريق قد رفضوا الصفر لانه يرمز للفراغ و العدمية وهم كانوا شعب يرفض الفراغ و العدمية رفضا تاما. ولكن ذلك الرفض الفلسفى لم يكن ذا قيمة بالنسبة لشعوب اخري كالهنود او لاصحاب الديانات اليهودية والمسيحية والاسلامية على سبيل المثال. ولكن الاعتراضات الرياضية كانت اكثر موضوعية. فخواص الصفر تختلف عن خواص باقى الاعداد. وعند التعامل مع الصفر تظهر بعض التعبيرات اللتى تمثل بعض الصعوبة فى مفهم مقاصدها. وسنتعرف اليوم على هذه التعبيرات والفرق بينها وهذه التعبيرات هي : كمية غير معينة وكمية غير معرفة.
لكن قبل ان نبدأ لابد من توضيح ثلاثة امور اساسية: الامر الاول انه لا معنى للكلام عن كمية غير معينة او كمية غير معرفة من دون تحديد عن اى مجموعة اعداد نتحدث. فوصف عملية رياضية بانها غير معرفة دون ان ننسب هذه العملية الى مجموعة اعداد محددة كمن يقدم لوحة رسم هندسية بدون مقياس رسم. والعمليات الرياضية قد تكون غير معرفة بالنسبة لمجموعة اعداد ولكنها قد تكون معرفة بالنسبة لاخرى والعكس صحيح. وفى موضوع اليوم سأتحدث عن مجموعة الاعداد الحقيقية وان اردت استخدام مجموعة اعداد اخرى سأخصها بالذكر في حينها. و الامر الثانى هو ان الرياضيات تسعى بكل جهدها لتجنب وجود اي تناقاضات فيها. فوجود اى تناقض فى اي جزء فى الرياضيات حتى لو كان بسيطا يهدد بالقضاء على الرياضيات كلها. والرياضيون يفخرون بان الرياضيات صحيحة بنسبة 100% وانها مبرهنة برهانا تاما وكاملا. اما النقطة الثالثة فهي ان العمليات الحسابية الاساسية هى عمليتا: الجمع والضرب. اما عمليتا الطرح والقسمة فهما العمليتان العكسيتات. ويشترط فى نتائج عمليتى القسمة والطرح الا تناقض نتائح عمليتي الضرب والجمع و الا نكون خالفنا النقطة السابقة اللتى تشير الى تجنب الرياضيات للتناقضات.
و سنقوم اولا بالتعرف على مفهوم الكمية الغير معينة. ومن اجل ذلك دعونا نقوم بالتجربة الذهنية التالية. نعلم ان الاعدادالحقيقية توجد كلها متراصة ومرتبة فوق خط الاعداد. ولكننا الان سنتخيل اننا حررنا الاعداد من اماكنها فوق خط الاعداد وانها توجد مبعثرة كجزر مورزعة على محيط مائي لا نهائي. و الان لنتخيل فريق كشافة يريد ان يقوم بعمل رحلة استكشافية بين الاعداد. وللانتقال بين جزر الاعداد هذه يمكن وضع الواح خشبية للمرور فوقها لنصل من عدد لاخر. ولنتخيل ان فريق الكشافة مزود بالات حاسبة تستطيع اجراء عمليتين فقط هما عمليتا الجمع والضرب. كما يحصل فريق الكشافة فى البداية على ورقة بتعليمات بالرحلة اللتى ينبغى عملها. مثلا لنتخيل ان فريق الكشافة واقف فى المربع رقم 1 وورقة التعليمات تحتوي على 3 خطوات: اولا اجمع 2 فوق رقم مربعك ثم انتقل الى المربع اللذى يحمل قيمة النتيجة الجديدة ثم اضرب النتيجة فى 2 ثم انتقل الى المربع اللذي يحمل النتيجة الجديدة. ثم بعد ذلك اضف 2 وانتقل مرة اخيرة الى المربع ذي النتيجة الجديدة. ولكن يجب على فريق الكشافة عند كل خطوة وضع اشارات لتأمين طريق العودة تماما كما يفعل الكشافة فى الحقيقة. فانهم عندموا يكتشفون طريقا جديدا غير مأهول فانهم يضعون علامات ليعلموا من اين اتوا ولكي يستطيعوا الرجوع مرة اخرى ولا يضلوا الطريق. لنرى ذلك الان تفصيلا: اولا فريق الكشافة يقف على المربع 1. باضافة 2 يحصلون على النتيجة 3. فيضعون لوحا من الخشب بين المربعين 1 و 3. ثم يضعون سهما يشير من 3 الى 1 ويكتبون فوقه ناقص 2 وبذلك يؤمنون طريق عودتهم. ثم تأتى الخطوة الثانية فيضربون حسب التعليمات 3 فى 2 بواسطة الالة الحاسبة ويحصلون على النتيحة 6. الان يضعون لوحا من الخشب يصل بين المربعين 3 و6. ثم يضعون كما سبق سهما يشير من 6 الى 3 ومكتوب فوقه: القسمة على 2 . ثم تأتى الخطوة الاخيرة يجمعون 2 زائد 6 فيحصلون على 8. فكما سبق يضعون لوحا من الخشب بين 6 و 8. ثم يضعون سهما من 8 الى 6 ويكتبون عليه ناقص 2. ثم تبدأ رحلة العودة. فعليهم الان انطلاقا من المربع 8 اتباع السهم المكتوب عليه ناقص 2. وبالفعل سوف يجدون سهما عند المربع 8 مكتو ب عليه ناقص 2 ويشير باتجاه 6. ومن 6 عليهم قسمة 2, وبالفعل هناك سهم عليه هذه العملية فيصلون الى المربع 3 . ومن المربع الاخير عليها حساب ناقص 2. وبالفعل هناك سهم مكتوب عليه ناقص 2 يشير الى المربع 1. فى النهاية سيعود فريق الكشافة الى النقطة اللتى انطلقوا منها بدون اية مشاكل!
كانت هذه العملية بلا مشاكل لانها كانت لا تحتوي على صفر. والان لنرى مثال اخر ولكن كما تتوقعون في هذ الحالة سوف نستخدم الصفر. ولنتخيل ان هناك فريقان للكشافة وليس فريقا واحدا. فريق يقف على المربع 1 اما الفريق الثانى يقف على المربع 2. وورقة التعليمات لدي الفريق الاول تفيده بان يجمع 2 فوق رقم مربعه ثم يضرب النتيجة فى صفر ثم يضيف الى النتيجة 4. اما الفريق الثانى فالتعليمات لديه تفيده بان يضيف 3 الى رقم مربعه ثم يضرب النتيجة فى صفر ثم يضيف 6 الى النتيحة. لنرى ماذا سوف يفعل الفريقان. الفريق الاول يجمع 1 زائد 2 فتكون النتيحة 3 فيضع لوحا خشبيا بين 1 و3 ويضع سهما لتأمين طريق عودته يشير من 3 الى 1ومكتوب فوقه ناقص اثنين. ثم يضرب 3 فى 0 فيحصل على صفر فيضع لوحا خشبيا بين 0 و 3 وسهما يشير من 3 الى صفر مكتوب عليه القسمة على صفر. ثم يجمع 4 فيضع لوحا خشبيا بين 0 و4 وسهما يشير الى صفر ومكتوب عليه ناقص 4. وماذا عن الفريق الثانى؟ . نفس المبدأ. سيضع اولا لوحا خشبيا بين 2 و 5 ويضع سهما من 5 الى 2 مكتوب فوقه ناقص 3 . ثم لوحا خشبيا بين 5 و 0 وسهما يشير الى خمسة مكتوب فوقه القسمة على 0 ثم لوحا خشبيا بين 0 و 6 وسهما يشير الى صفر وفوقه مكتوب ناقص 6. الان نعود للفريق الاول مرة اخرى فبعد استراحة قصيرة يقرر الفريق العودة. وهو كما علمنا يقف الان عند المربع 4 ولكي يعود ادراجه عليه طرح 4 ثم القسمة على صفر ثم طرح 2 مرة اخرى. اولا سيجد سهما مكتوب فوقه ناقص 4 يشير الى 0. فينتقلون الى المربع صفر. الان عليهم اتباع السهم المكتوب فوقه القسمة على صفر. ولكنهم الان سيجدون سهمين مختلفين مكتوب عليهما القسمة على صفر. احد السهمين يشير الى 3 بينما الاخر يشير الى خمسة. والسهم الاول قد صنعوه هم بانفسهم اما السهم الاخر فقد صنعه الفريق الاخر. فاذا افترضانا ان فريق الكشافة قصير الذاكرة جدا و انه لا يتذكر اي سهم قد صنع. فقط هو يتذكر اللحظة الراهنة وورقة التعليمات اللتى امامه. فانه لن يدري اى طريق عليه ان يختار . واذا اختار الطريق الخاطئ واتجه نحو 5 . فيجد عليه الان اجراء عملية طرح ناقص 2. فاذا افترضنا انه وجد عند المربع 5 اشارة مكتوب عليها ناقص 2 صنعها فريق كشافة ثالث فى وقت سابق فانها سوف تشير الى المربع 3. فسوف يذهب فريق الكشافة الى هذا المربع ويكون ضل طريقه الى الابد ولن يكون بامكانه العودة ابدا الى المربع 1 اللذى ابتدأ منه رحلته!!
كان هذا المثال يشير الى فلسفة فكرة الكمية الغير معينة. ويوضح المثال ان كنه مشكلة العمليات الغير معينة ان هناك اكثر من احتمال ممكن للعملية الرياضية محل الاعتبار. فمعنى عملية قسمة صفر على صفر هى انى ابحث عن عدد اذا ضربته فى صفر اعطانى صفرا. فالعملية فى حد ذاتها لها معنى ولكن ليس هناك حلا واحد ولكن حلولا عديدة لها. ولهذا فان هذه العملية غير معينة. فالعمليات الحسابية لا ذاكرة لها. فهى اشبه بحالة الهيام الصوفى وهى دائما موجودة فى ملكوت نفسها و لا تدرك او تعتمد على اي شئ اخر. فمثلا اذا سألتنى ماقسمة 6 على 3 سأجيبك 2 فورا ولن اسالك لماذا تسال هذا السؤال؟ هل تريد مثلا توزيع 6 دولارات على 3 اشخاص. او ان عندك قطعة ارض مساحتها 6 هكتارات وانت تريد تقسيمها الى 3 قطع متساوية المساحة. وهكذ الحال فى قسمة صفر على صفر هى عملية قائمة فى ذاتها لكنى لن استطيع ان اعطيك ردا نهائيا حاسما اذا سالتنى ما قسمة صفر على صفر. ومن هنا تظهر الحاجة الىى اكتشاف عملية رياضية جديدة تتمتع بذاكرة رياضية. فمثلا تقول فى حالة المثال السابق اذا كنت تتبع المسار الاول ووجدت عملية قسمة صفر على صفر فاتجه الى 3 اما اذا كنت تتبع المسار الثانى ووجدت صفر على صفر فاذهب الى 5. وهذه العملية ذات الذاكرة اللتى تعتمد على المسار والنقاط المجاورة هى عملية حساب النهايات. وبناء على ذلك فان الدالة
y = (x^2 +x-2)/(x-1) 1
اذا عوضنا قيمة x بواحد فاننا سنحصل على صفر على صفر. مما يعنى ان اعطاء نتيحة لقيمة الدالة عند هذه النقطة هى عملية غير ممكنة لكن حساب النهايات يخبرنا انه كلما اقتربت قيمة x من واحد ستقترب قيمة y من 3 ويمكنكم التأكد بانفسكم بالتعويض في قيمة x ب 0.99999 او 1.00001 !!
كان هذا عن العملية الغير المعينة. لكن ماذا عن العملية الغير معرفة؟ العملية الغير المعرفة هى عكس العملية الغير المعينة. بمعنى انه فى العملية الغير معينة كانت هناك اكثر من اشارة لنفس العملية اى قسمة صفر على صفر. اما العملية الغير معرفة فانني لن اجد اي اشارة على الاطلاق لهذه العملية. اذا اتخيلنا مثلا ان التعليمات لدي فريق الكشافة الموجودة فى المربع 1 تخبره بان يقسم 1 على صفر ويتجه الى المربع اللذي يحمل قيمة تساوي قيمة النتيحة. وكما نعلم فى عمليات القسمة يجب على فريق الكشافة البحث عن اشارة تتناسب مع هذه العملية. فانه لن يجد اى اشارة تشير الى قسمة واحد على صفر حتى لو افترضنا انه كانت هناك فرق للكشافة لانهائية قامت بتعبيد كل الطرق اللانهائية الممكنة ووضعت اشارات العودة عليها. ودعونا نرى الان لماذا الاتوجد اشارة تشير الى قسمة واحد على صفر. اولا لاننا كما قلنا ان عملية القسمة هي عكس عملية الضرب. فمعنى انني اقوم بقسمة 1 على صفر هو انى ابحث عن عدد حقيقى عندما اضربه فى صفر تكون النتيجة 1. ونحن نعلم ان هذا العدد لا يمكن ان يكون موجودا. لانه من خواص الصفر ان ضرب اى عدد حقيقى في صفر يعطى صفرا. و الامل الوحيد المتبقى لحل هذه العملية ان يكون العدد اللذى نبحث عنه عددا ليس حقيقيا. ولكننا قلنا من البداية اننا محصورون فى نطاق الاعداد الحقيقية.
ويمكننا تعميم الامر فنقول ان قسمة عدد غير الصفر على صفر يعطى كمية غير معرفة فى نطاق الاعداد الحقيقية ولكن قسمة صفر على صفر يعطى كمية غير معينة. ولكن حيث اننا نعيش فى عالم عجيب تعتراه الفوضى والتضارب احيانا. فان هناك بعض كتب الرياضيات اللتى تقول ان قسمة اى عدد مهما كان على صفر هى عملية غير معرفة وبهذا تجعل من قسمة صفر على صفر عملية غير معرفة وغير معينة فى نفس الوقت. ولكنى انا شخصيا غير مقتنع بهذا التوصيف وراينا فى اعلى السبب. كما ان معظم الكتب الرياضية ترفضه ايضا
اذن فمعنى عملية غير معرفة انها عملية مستحيلة لا معنى لها و لا حل لها ومعنى عملية غير معينة بانه هناك اكثر من احتمال لحل هذه العملية. ويمكننا تشبيه الامر الى حد ما بحل منظومة المعادلات الخطية. ققد يكون هناك حل وحيد او عدد لانهائى من الحلول او لا حل على الاطلاق. وهكذا يكون الحال فان كان هناك حل وحيد فان العملية تكون معينة ومعرفة. اما اذا لم يكن هناك اى حل فانها تكون غير معرفة اما اذا كان هناك اكثر من حل فان العملية تكون غير معينة. وهناك امثلة كثيرة للعمليات الغير معرفة. مثال على ذلك قسمة 7 على 3 فى نطاق الاعداد الطبيعية. فكما نعلم لا يوجد اى عدد طبيعى اذا ضربناه فى 3 تكون النتيجة 7 . وحيث انه لاحل لهذه العملية فهي غير معرفة. ولكن قيمة حل هذه العملية ينتمى الى نطاق الاعداد النسبية. فلذلك قسمة 7 على 3 غير معرفة فى الاعداد الطبيعية والصحيحة لكنها معرفة ضمن الاعداد النسبية و الحيقيقية. مثال اخر عملية حساب الجذر التربيعى لسالب 1 فى نطاق الاعداد الحقيقية. هذه العملية غير معرفة لانه لا يوجد حل لهذه العملية. فلا يوجد عدد حقيقى سواء كان موجبا او سالبا او صفرا اذا ضربناه فى نفسه يعطى نتيجة سالبة. ولكن مع ذلك فان هذه العملية بعينها معرفة فى نطاق الاعداد التخيلية والمركبة.
و الان دعونا نفعل شئيا مثيرا جديدا. دعونا نوسع الاعداد الحقيقية لجعل عملة القسمة على صفر ممكنة ومعرفة. فكما ان الاعداد التخيلية جعلت عملية اخذ الجذر التربيعى للاعداد السالبة معرفة وممكنة رغم اعتراضات المعترضين اللذين قالوا ان هذا شئ سخيف لامعنى له ولا فائدة ابدا من وراءه. فان الاعداد التخيلية لها مكانتها الهامة جدا اليوم خصوصا فى مجالات التطبيقات الفيزيائية. كذلك الحال بالنسبة للصفر. فاننا نعلم ان قسمة اى عدد بخلاف الصفر على الصفر يعطى مالانهاية. وأن هذه العملية غير ممكنة قانونيا فى نطاق الاعداد الحقيقية لانه كما نعلم ان المالانهاية لا ينتمى الى مجموعة الاعداد الحقيقية.
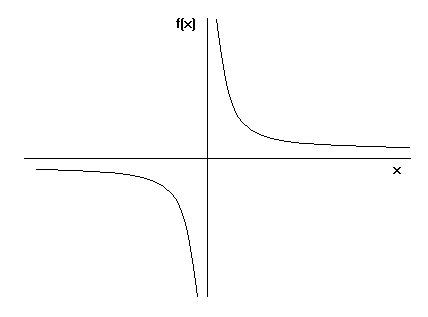
اول خطوة ينبغى علينا عملها هو توسيع مجموعة الاعداد الحقيقية. بان نضم عليها عددين جديدين هما موجب مالانهاية وسالب مالانهاية. ونحن لا نستطيع الان ان نطلق على مجموعة الاعداد الجديدة اسم مجموعة الاعداد الحقيقية ولكن سوف نطلق عليها مجموعة الاعداد الحقيقية الموسعة. والان لنعرف الخواص الرياضية للمالانهاية الموجبة والسالبة. فنجد ان جمع مالانهاية زائد اى عدد اخر يعطى مالانهاية ولكن جمع مالانهاية زائد سالب مالانهاية هو عملية غير معينة وضرب المالانهاية الموجبة مع اى عدد موجب يعطى مالانهاية موجبة وضرب مالانهاية موجبة مع اى عدد سالب يعطى مالانهاية سالبة وضرب مالانهاية فى صفر عملية غير معينة لانه يساوي تماما قسمة صفر على صفر. وقد رأينا عاليا انها عملية غير معينة. والمثل بالنسبة للمالانهاية السالبة. اذن فقد جعلنا الان المالانهاية عددا عاديا ينتمى الي مجموعة الاعداد الحقيقية الموسعة. الان نريد ان نرى ماذا تعطى عملية قسمة 1 على صفر. هناك احتمالان ممكنان لقسمة واحد على صفر. هما موجب مالانهاية وسالب مالانهاية. من الرسم الموجود اعلى نرى ان اننا عندما نتحرك قيد انملة باتجاه يمين العدد صفر فان نهاية الدالة (1/x) هى موجب مالانهاية اما اذا تحركنا قيد انملة باتجاه اليسار فتكون النتيجة سالب مالانهاية, اي ان هناك احتمالان لقسمة واحد على صفر . اى اننا صحيح اننا جعلنا العملية معرفة ولكنها مازالت غير معينة. ونحن الان نريد تعيينها. فبامكانى الان مثلا ان اقول ان قسمة 1 على صفر تساوي موجب مالانهاية تعريفا وقانونا. وبهذا اكون قد وجدت صياغة رياضية سليمة لقسمة واحد على صفر. ولكن عمل مثل هذا هو رياضيا جائز وهذا ما فعله ريمان بالمناسبة ولكنه ليس دائما حكيم. لاننى بهذا سافقد نصف الحلول الاخرى اللتى تعطى سالب مالانهاية. كما انه ليست هناك ضرورة منطقية لكى تعطى قسمة واحد على صفر موجب مالانهاية فقط. و نلاحظ ان الفارق بين موجب مالانهاية وسالب مالانهاية هو فى اللاشارة فقط . بمعنى اننى اذا اخذت القيمة المطلقة لقسمة واحد على صفر فانني سوف احصل فى جميع الاحوال على موجب مالانهاية. وهذا هو التعريف الرسمى لقسمة اى عدد بخلاف الصفر على الصفر ضمن نطاق مجموعة الاعداد الحقيقية الموسعة . وهو ان القيمة المطلقة لقسمة اى عدد بخلاف الصفر على صفر يعطى موجب مالانهاية!!



جزاك الله خيرا على ماقدمته لنا من إفادة
لك جزيل الشكر على كل مقالاتك ,وأسأل الله العلي القدير أن يكافئك في الدنيا واالأخرة.
مشكور, مبدع