نصل اليوم الى المحطة الاخيرة في قصة تطور الصفر في العصور القديمة. وتاريخ تطور الرياضيات طويل وممتد من العصر الحجرى مرورا بمصر الفرعونية ثم تطورت الاعداد على ارض بابل ثم فى بلاد الاغريق. وكان لفيثاغورث وزينون وديموقريط كما رأينا دورا هاما في تطور الرياضيات واثراء الحضارة الانسانية.

وقد بلغت الدولة الاغريقية اقصى مدى لها في عصر الاسكندر الاكبر حيث قام بغزوات حربية واسعة غزى فيها معظم اراضى العالم القديم. فشملت مملكة الاسكندر الاكبر: اليونان وايطاليا ومصر وبابل وايران وبعض اجزاء من الهند. ولكن الاسكندر توغل اكثر من اللازم فتذمر جنوده وتمردوا عليه وطلبوا العودة. فاذعن الاسكندر وهو كاره ولكنه في طريق العودة مرض وقضى نحبه. وبعد وفاة الاسكندر طمع قادة جيشه في ملكه فقتلوا زوجته روكسانا وابنه وهو طفل صغير حتى لا ينازعهم احد من عائلة الاسكندر الحكم. واقتسم قادة جيش الاسكندر الاربعة مملكته وحولوها الى اربع ممالك متنازعة ومتناحرة. فكانت المملكة الاولى تشمل بلاد اليونان وايطاليا. والمملكة الثانية تشمل البلاد الواقعة في اسيا الصغرى والمملكة الثالثة تشمل سوريا والعراق والمملكة الرابعة تشمل مصر وفلسطين. ثم سقطت هذه الممالك الواحدة تلو الاخرى امام الرومان. وكانت المملكة المصرية هى اخر الممالك الاغريقية اللتى سقطت  وكانت كليوباترا اخر ملكة هيلينية في التاريخ القديم. ويخطئ الكثيرون عندما يتصورون ان اثينا كانت عاصمة اليونان الحضارية وانها كانت اهم مدنها. بل ان الاسكندرية المصرية كانت في واقع الامر هى اهم العواصم الاغريقية حضارة وكانت مكتبة الاسكندرية صرحا علميا هائلا لايدانيها فى ذلك دانى. ويكفى للتدليل على اهمية دور علماء الاسكندرية فى تطور الحضارة الانسانية ان نذكر اسما واحدا وهو اقليدس اللذى يدرس تلاميذ المدارس اليوم في كل انحاء الكرة الارضية الهندسة المسماة باسمه: اى الهندسة الاقليدية.

وسنتعرف اليوم على عالم اغريقى وهو ارشميدس اللذي عاش فى جزيرة صقلية في الفترة اللتى سبقت سقوطها مباشرة على يد الرومان. وقد ولد ارشميدس في جزيرة سامو وهى نفس الجزيرة اللتى ولد فيها فيثاغورث وكان ذلك بعد مائتى سنة من ميلاد زينون صاحب المفارقة الهامة. وقد عاش ارشميدس فترة طويلة في مدينة الاسكندرية. ودرس الرياضيات في مكتبتها. ثم  التحق ارشميدس بعد ذلك  ببلاط ملك مدينة سراكيوز في جزيرة صقلية حيث عمل كمستشار علمى. وفى احد المرات كلفه الملك بمهمة في غاية الصعوبة. فقد اراد الملك ان يعرف هل ان تاجه مصنوع من الذهب الخالص ام ان الصائغ قد غش في الخامات وخلط الرصاص مع الذهب. وكانت هذه مهمة في غاية الصعوبة تفوق طاقة العلماء في ذلك العصر. وكانت هذه المشكلة مستحوذة على تفكير ارشميدس طوال الوقت. وتقول الرواية انه في احدى المرات عندما كان ارشميدس مستلقيا فى حوض الاستحمام طرأت له فكرة ثورية. فقد انتبه الى انه عندما يكون حوض الاستحمام مملوئا حتى حافته ثم نضع فيه جسما ما. فان الماء ينسكب من حافة حوض الاستحمام ويكون حجم الماء المنسكب مساويا لحجم الجسم المغمور . وهذا هو اهم مبادئ الهدروستاتيك. اللذى يقول ان اى جسم مغمور بشكل كامل او جزئى فى الماء يتعرض لضغط يساوى وزن الماء المزاح. وفكر ارشميدس ان يستغل حجم الماء المسكوب فى تعيين كثافة الجسم المغمور في الماء وبالتالى تحديد نوعية المادة المتكون منها ذلك الجسم. وبهذا يستطيع ارشميدس ان يحدد اذا كان تاج الملك مصنوع من الذهب الخالص ام لا. وقفز ارشميدس الى الشارع وهو يصرخ فرحا يوريكا يوريكا بمعنى وجدتها وجدتها. ولم ينتبه ارشميدس من شدة فرحته انه كان متجردا من ثيابه تماما!!

لكننا لم نذكر ارشميدس اليوم من اجل تلك القصة ولكننا ذكرناه لسبب اخر يتعلق بالصفر والمالانهاية ومفارقة زينون. فقد كان ارشميدس اقرب انسان فى التوصل الى حل صحيح لمفارقة زينون. ولكننا يجب ان نؤكد ان حل ارشميدس لم يكن صحيحا تماما ولكنه كان اقرب حل للرياضيات اللتى نستخدمها اليوم.

كان ارشميدس معنيا بدراسة المرايا المقعرة ولاحظ ارشميدس ان المرايا اللتى لها شكل قطع مكافئ تركز اشعة الضوء فى بؤرتها تماما. وهذه ربما تكون اشارة لاتحاد المالانهاية مع الصفر. فاشعة الشمس المتوازية اللتى تأتى من مسافة بعيدة او المالانهاية تنعكس على سطع المرأة المقعرة لتتجمع فى الصفر او فى نقطة البؤرة. ولكن كان هناك سؤال لم يستطع رياضيو الاغريق الوصول الى اجابة اليه: وهو كيف يحسب الانسان مساحة  القطع المكافئ. فقد عرف الاغريق كيف يحسبون مساحة المثلث او الدائرة ولكنها عجزوا عن ايجاد علاقة لحساب مساحة القطع المكافئ.

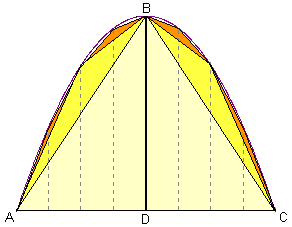
وتوصل ارشسميدس الى  طريقة لحساب مساحة القطع المكافئ. ولكن هذه الطريقة كانت شديدة الغرابة وعارضها رياضيو الاغريق مع ان الطريقة كانت تعطى نتيجة دقيقة جدا. ارشميدس قال سنقرب شكل القطع المكافئ الى اكبر مثلث يمكن رسمه فى حيز فراغ  القطع المكافئ. وكما هو موضح بالرسم فان هذا المثلث هو المثلث ABC. وافترض ارشميدس ان مساحة هذه المثلث X.  ونلاحظ انه بعد رسم هذا المثلث فان هناك فراغان صغيران ينشئان يمين ويسار المثلث الكبير. والان نعيد الكرة وفى كل فراغ نحاول ان نرسم اكبر مثلث يملأ مساحة ذلك الفراغ. فنحصل على مثلثين صغيرين. استطاع ارشمسيدس ان يوضح ان مساحتهما معا هى X/4. ولكن ينشأ بعد ذلك فراغات اصغر ممكن ان نرسم فيها مثلثات جديدة على نفس النسق السابق تكون مساحتها X/16. وتستمر هذه العملية الى مالانهاية ولكن فى كل مرة فان مساحات المثلثات الجديدة تقل حتى تكاد تنعدم. وقال ارشمسيدس ان مجموع مساحات المثلثات النهائية وبالتالى مساحة القطع المكافئ هى 4X/3. وهذه نتيجة دقيقة جدا وتتفق مع حساباتنا اليوم.

لكن معاصرى ارشميدس من الرياضيين الاغريق رفضوا هذه الطريقة وانتقدوها وقال ان اللعب مع المالانهاية بهذا الشكل امر مرفوض وانه لايمكن ان يكون مجموع عناصر لانهائية قيمة محدودة. وارشميدس نفسه اتفق معهم وقال انه يرفض وجود المالانهاية وانه لا يجرى عملية الجمع حتى المالانهاية ولكنه يجريها حدد محدود من المرات. ولكن هذا العدد المحدود كاف لكى تقترب نتيجته من الاجابة الصحيحة. وباختصار فان موقف ارشميدس يمكن تلخيصه فى الثلاث نقاط التالية:

1 قال ان مجموع عدد لانهائى من المثلثات مرسومة فى الفراغ اللذى يشغله حيز القطع المكافئ هو رقم محدود
2 رفض ارشميدس المالانهاية وقال انها غير موجودة
3 رفض ارشميدس الصفر وقال انه غير موجود

وقد وضع ارشميدس تعريفا للاعداد يستبعد الصفر من خلاله. فقد قال ارشميدس ان اى عدد مهما كان صغير اذا جمعناه الى نفسه عدد كبير من المرات فانه سوف يصبح في النهاية اكبر من اى عدد معروف اخر. وهذا التعريف يستبعد الصفر . لاننا مهما جمعنا الصفر الى نفسه فاننا لن نحصل سوى على صفر.

باختصار كان رفض ارشميدس و الاغريق للصفر والمالانهاية قاطعا. وكان ذلك يمثل نهاية لامكانية تطور الرياضيات بعد ذلك. فلا يمكن للرياضيات ان تتطور بدون وجود الصفر. ولو قبل الاغريق الصفر وهى البلاد العاشقة للرياضيات لكان من الممكن ان يتوصلوا الى حساب التفاضل واشياء اخرى هامة. ولكنهم لم يفعلوا ذلك. وكان هذا يمثل عمليا المحطة الاخيرة للرياضيات في الحضارة الاغريقية.

يبقى لنا ان نذكر نهاية ارشميدس . وكما علمنا فان فى ذلك الزمان كانت الحرب مندلعة بين الاغريق والرومان. وكان ارشميدس اسما لامعا فى سماء تلك الحرب. فقد صنع الات حربية متفوقة جدا وذات افكار غريبة. وكان مجرد ذكر اسم ارشميدس يصيب الجنود الرومان بالفزع. فقد استخدم ارشميدس مرايا عاكسة عملاقة لكى تحرق سفن الرومان وهى فى عرض البحر. كما انه تمكن من تطوير الات رفع هائلة يمكنها رفع سفن الرومان في الهواء ثم تركها لتسقط على مقدمتها فتغرق فى الحال فى وسط البحر. كما انه اخترع مقاليع هائلة لقذف الرومان بالحجارة. وكان الرومان يصابون بالهلع كلما شاهدوا لوح خشب او حبل عائم فوق سطح الماء. فانهم كانوا يظنون ان هذه حيلة جديدة من حيل ارشميدس.

لكن في احد الايام استطاع الرومان استغلال غفلة حراس مدينة سراكيوز واقتحموا المدينة على حين غفلة من اهلها. وتفاجأ الجميع بوصول الرومان الى قلب المدينة. وكان ارشميدس عند الشاطئ يحاول حل مسألة رياضية على الرمال  كما كانت هى عادة رياضيي الاغريق. فلم يتعرف عليه جندى رومان طلب منه ان يمضى معه. وقد كان ارشميدس فى ذلك الوقت رجلا كبيرا فى العمر سنه 75 سنة غير معنى بمظهره الخارجى وكان ارشميدس قد اصيب بشبه عمى نتيجة دراسته لكسوف الشمس وتطلعه اليها بدون وسائل حماية. ورفض ارشميدس ان يمضى مع الجندى الرومان لانه لم ينتهى من حل المسالة بعد. فطعنه الجندى الرومانى بنصل رمحه فقضى عليه. وهناك مقولة خبيثة تقول ان انجاز او صنيعة الرومان الوحيدة في الرياضيات هى انهم قتلوا ارشميدس!!

وقد تمكن الرومان بعد ذلك من غزو مصر. وانتحرت كليوباترا اخر ملكة هيلينية متبقية. واحترقت مكتبة الاسكندرية على يد يوليوس قيصر اولا  والرومان بعد ذلك فى محاولات غزوهم مصر. ثم اتت الجماهيرالدهماء على البقية الباقية من مكتبة الاسكندرية فى احداث مقتل الفيلسوفة هيباثيا. وكان في ذلك خسارة للبشرية كلها. ولم تكن للحضارة الرومانية انجازات علمية تذكر. فالرومان كانوا امة عسكرية بصفة خاصة برعوا فى الامور العسكرية والسياسية والادارة. وربما ظهر من بين الرومان بعض المؤرخين ولكن لم تقدم الحضارة الرومانية للعالم شيئا علميا مفيدا يذكر. ولم تتطورالرياضيات في عهد الرومان بل تراجعت. وفى هذه الاثناء انتقلت شعلة الحضارة الى الشرق حيث الهند والبلاد الاسلامية.