قنع الرياضيون لفترة طويلة بمفهوم المالانهاية الممكنة او المالانهاية بالقدرة. ولم يهتموا بالمالانهاية الحقيقية أو المالانهاية بالفعل. وهناك فارق اساس بين المفهومين. فالمالانهاية الممكنة هي قيمة أعجازية هائلة لا يمكن لأي عدد حقيقى معين أن يصل أليها. وهى تمثل سقف الأعداد الحقيقية -اللتى لانهاية لها-. مع ذلك يجب علينا ان ننتبه أنها مازالت تنمي لنطاق الأعداد الحقيقية. بيد أنها فى نفس الوقت تعبر عن فكرة لا يمكن تجسيدها فى عدد حقيقى معين بذاته. فكل عدد حقيقي هناك عدد أخر أكبر منه.  ويمكننا تشبيه ذلك بأفق كوننا اللذي يتمدد الي مالانهاية – في حالة كون كوننا لانهائيا-. فنحن مهما فعلنا لا يمكننا أن نصل الي أفق كوننا أبدا. لكن أفق كوننا مازال ينتمي الى كوننا. فأفق كوننا يمثل المالا نهاية الممكنة اما المالانهاية الحقيقية فهى تقع خارج نطاقه . لكن بفرض اننا وصلنا الى أفق كوننا. فماذا يأتى خلفه؟ لاشئ؟ ام ربما يبدأ كون جديد؟ بالمثل فبعد الأعداد الحقيقية اللتى لانهاية لها يبدأ عالم المالانهاية الحقيقية او المالانهاية بالفعل. وكان أول من دخل هذا العالم الرياضى الأستثنائي جيورج كانتور. وسنحاول اليوم التعرف علي أهم أفكاره.

اذن السؤال الأن: هل المالانهاية الحقيقية لها وجود فعلا؟  ام انها كالغول والعنقاء خرافات لا وجود لها. ونحن طبعا عندما نسأل عن وجود المالانهاية لا نقصد ذلك من الناحية الفلسفية او الدينية او الفيزيائية. لكن من الناحية الرياضية البحتة. كانت اجابة كانتور على هذا السؤال قاطعة بنعم وكانت انطلاقته من نظرية المجموعات. فهناك مفهوم يعرف بسعة أو ضخامة المجموعة أو ال cardinality . وهو يعبر عن عدد العناصر الموجودة بداخل المجموعة. فمثلا مجموعة تحتوي ثلاثة كلاب سعتها ثلاثة ومجموعة مكونة  من خمس تفاحات سعتها خمسة وهكذا. لكن ماذا عن مجموعة الأعداد الطبيعية؟. نعلم ان مجموعة الأعداد الطبيعية لها بداية هى العدد صفر أو العدد واحد حسب المدارس الرياضية المختلفة. لكن مجموعة الأعداد الطبيعية لا نهاية لها. بمعنى انه لا يوجد عدد طبيعى محدد هو نهاية الأعداد الطبيعية. اذن ما هو عدد الأعداد الموجودة فى مجموعة الأعداد الطبيعية؟ او بصياغة ادق ما هي سعة مجموعة الأعداد الطبيعية؟ بالطبع لا يوجد عدد طبيعى يعبر عن هذه السعة لانه كما سبق وقلنا لا يوجد عدد طبيعى يمثل سقف مجموعة الأعداد الطبيعية. اذن لابد من اختراع عدد من نوع جديد. من نوع المالانهاية.

وأطلق كانتور على اسم عدده الجديد اسم ألف صفر. وأختار الألف لانه أول الحروف  الأبجدية فى اللغة العبرية كما هو فى اللغة العربية.  ويمكننا ان نعتبر هذا الاختيار قرينة على أصول كانتور اليهودية. علاوة عل ذلك فأختيار الأسم يوحي بشئ أخر. فالكتاب المقدس يبتدئ بقسم يهودي وهو العهد القديم اللذي يبدأ تحديدا بسفر التكوين اللذي يحكي قصة الخلق فى العقيدتين اليهودية والمسيحية. لذلك ربما اراد كانتور ان يشير الى انه قد خلق عوالم رياضية جديدة . ابتدأها بأول عالم: العالم ألف صفر. وكان الرياضى النابغة هلبرت من اشد المعجبين باعمال كانتور المتعلقة بالمالانهاية وقال عنها: لن يستطيع أحد بعد اليوم ان يخرجنا من الجنة اللتى ادخلنا كانتور أياها.

اذن ملخص ما سبق هو أن تعريف المالانهاية ألف صفر هى أنها سعة مجموعة الأعداد الطبيعية. ولاشك ان هذه كانت لفتة ذكية من كانتور. لكن مع ذلك يبقى الأمر حتى الأن مملا فمثل هذه النتيجة لابد وأن خطرت بخاطر رياضيين كثيرين خلاف كانتور. بل ولا أستبعد ان تكون تلك الفكرة قد وردت فى عقول بعض قراء هذا المقال من قبل حتى وان لم تكن لهم دراية بموضوع المالانهاية كما فصله كانتور. ولكى يكون للموضوع أهمية ما لابد من استنباط  بعض خواص المالانهاية الحقيقية. اذن لابد من وسيلة نستطيع من خلالها ان نقارن بين سعات المجموعات اللانهائية المختلفة.

كيف يمكننا ان نقارن بين سعات المجموعات اللانهائية المختلفة؟ دعونا نفعل ذلك بمساعدة المجموعات المنتهية ثم نعمم النتيجة على المجموعات اللانهائية. دعونا نتخيل استادا او ملعبا لكرة القدم. ودعونا نفترض أن علينا أجابة سؤال : ما اللذي هو أكثر عددا؟ المقاعد الموجودة؟ أم الجمهور؟ يمكنننا أن نبدأ بعد المقاعد الموجودة فنجدها مائة ألف مثلا. ثم نبدأ فى  عد الجمهور فان  كان أكثر من عدد الكراسى كانت عدد الجمهور أكبر. وأن  كانت المقاعد أكثر كان العكس صحيح. وأن لم يكن هذا أو ذاك فهم مستاوون. لكن لا شك ان هذه الطريقة تستغرق وقتا طويلا. فماذا اذا كانت مجموعة المقاعد والجماهير لانهائية. بالطبع اننا لن نستطيع من الأنتهاء من عد مجموعة واحدة ناهيك عن الأثنين ثم المقارنة بينهما.

أذن دعونا نفكر فى طريقة أخرى. دعونا نبتكرا شيئا تنظيميا معينا نجعل من خلاله لكل فرد من الجمهور كرسى معينا يناسبه. مثلا أن نعطى لكل فرد من الجمهور بطاقة دخول تحوى رقما معينا فريدا ونطلب  منه ان يجلس على نفس المقعد اللذي يحمل نفس الرقم. وبعد الانتهاء من هذا ألأمر وتوزيع الجمهور على المقاعد. يمكننا بنظرة واحدة ان نرى ان كان هناك مقاعد خالية فان عدد المقاعد أكثر من عدد المتفرجين. وأن بقى بعض الجمهور واقفا فان معنى ذلك أن عدد الجماهير أكبر. وان لم يكن هذا ولا ذاك فهم متساوون فى السعة أو  العدد.!

ولمقارنة سعتي مجموعتين لانهائيتين دعونا نتبع نفس الخطة السابقة. فعلينا اولا ان نبتكر طريقة تنظيمية معينة نناظر من خلالها كل عنصر من المجموعة الأولي بعنصر مقابل من المجموعة الثانية. ثم ننظر فى النهاية هلى يبقي أي عنصر من أي مجموعة من دون نظير من المجموعة الثانية. فان كان هذا لكان معناه ان المجموعتين ليستا متساويتان فى السعة. وعلينا ان نلاحظ ان ابتكار تلك الطريقة التنظيمية لمناظرة عناصر المجموعة الاولي بعناصر المجموعة الثانية هي أختبار ذكاء حقيقي للرياضى اللذي يجري هذه الأمر. وبناء على هذا الأمر دعونا نرى بعض الخصائص اللتى اكتشفها كانتور حول المجموعات اللانهائية.

كانت اول خاصية اكتشفها كانتور وأن كان قد سبقه اليها جاليليو هي ان الجزء ليس دائما اصغر من الكل فى المجموعات اللانهائية. او بصياغة اخرى ان سعة مجموعة جزئية لانهائية ليست بالضرورة أقل من المجموعة الأم. لنرى ذلك دعونا نقارن مجموعة الأعداد الطبيعية 1 و 2 و3 و4 و 5 الي أخره بمجموعة جزئية منها وهى مجموعة الأعداد الطبيعية المزدوجة ك 2 و 4 و 6 و 8 و 10 الى أخره. ودعونا نتخيل اننا اوقفنا مجموعة الأعداد الطبيعة صفا واحدا. ثم ضربنا كل عدد فى 2 . فسنحصل على عدد مزدوج فريد من مجموعة الاعداد الطبيعية المزدوجة. وباتباع هذه الطريقة التنظيمية لن يبقى اى عدد من المجموعة الأم بدون قرين فريد من مجموعة الأعداد المزدوجة! ثم بالمثل دعونا نصف مجموعة الأعداد المزدوجة صفا واحدا . ثم دعونا نقسم كل عدد مزدوج على 2 . مرة أخرى سنحصل دوما على عدد طبيعى فريد. ولا يوجد عدد مزدوج بدون قرين له من المجموعة الأم. اذن مجموعة الأعداد الطبيعية ومجموعة الأعداد المزدوجة متساويتان فى السعة!

ربما كان هذا مثالا يسيرا. دعونا نرى امرا أخر أكثر صعوبة. دعونا نقارن بين سعة مجموعة الأعداد الطبيعية بسعة مجموعة الأعداد النسبية. البديهة تقول ان الأعداد النسبية أكثر عددا. دعونا مثلا نري الكسور الموجودة بين الصفر والواحد.  فالكسور الممكنة هى 1/2  أو 1/3 أو 1/4 الي أخره. أى ان هناك مالانهاية من الكسور الممكنة بين العددين صفر و واحد. وهكذا الحال بين أى عددين طبيعيين أخرين فيمكننا ان نجد مالانهاية من الكسور المنحصرة بينهما. لكن هل الطريقة المنهجية المنظمة تدعم هذه النتيجة البديهية. علينا ان نبتكر أولا ألية نناظر من خلالها الأعداد النسبية بالطبيعية. ودعونا هنا نرى ذكاء كانتور. فقد ابتكر الطريقة التالية:

مناظرة الأعداد النسبية بالطبيعية

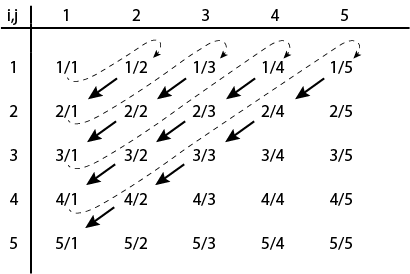
حيث أن الاعداد النسبية هى عبارة عن نسبة  بين عددين صحيحين. فيمكننا كتابة كل الأعداد النسبية فى صورة جدول من صفوف وأعمدة كما فى الرسم . ثم بأعادة صف تلك الأعداد كما بالصورة يمكننا ان نناظر كل عنصر من عناصر الأعداد النسبية بعنصر من الأعداد الطبيعية. اي ان سعة الأعداد النسبية ليست أكبر من سعة الأعداد الطبيعية. بل أنها تساويها عكس ما توحي به البديهة.

الأن هل يمكننا مما سبق ان نستنتج ان كل المجموعات اللانهائية متساوية فى السعة؟ لو كان هذا الأمر صحيحا لكان موضوع المالانهاية مملا ولا توجد اهمية كبيرة لدراسته. لكن كانتور اكتشف اشياء عجيبة فليست كل المجموعات اللانهائية متساوية فى السعة. بل أن هناك مجموعات سعتها أكبر من سعة مجموعة الأعداد الطبيعية. لكن ذلك سوف نراه في المرة القادمة أن شاء الله.