تصف قوانين الفيزياء عالمنا و حوادثه بمنتهى الدقة.  او على الاقل فهى تحاول ذلك. ولذلك اذا اردنا البحث عن تطيبقات قوانين الفيزياء فليس علينا الذهاب الى المختبر او الغوص فى اعماق مئات من صفحات كتب الفيزياء. لا. بل علينا فقط ان نفتح اعيننا جيدا وننظر حولنا. فكل ما يحدث حولنا هو تطبيق مباشر لقوانين الفيزياء. لا عب كرة قدم يسدد ضربة جزاء او طفل يلهو بفقاعات الصابون. كل هذا تصفه قوانين الفيزياء. و الامر الرائع ان الفيزياء تعامل كل الامور بنفس المعيار. تافهة كانت او مهمة. فهى تقيس الامور بنفس المسطرة وتزنها بنفس المكيال. وفى حقيقة الامر فانه لا يوحد امر نستطيع ان نصفه بالتافه واخر بالمهم. قكل عالمنا ساحر وبديع. ولكنها لعنة الرتابة و الاعتياد اللتى تضع غشاوات سميكة فوق اعيننا فلا نعد نستطع ان نرى الجمال ونقدره. وتكون سعادتنا شديدة عندما ينقشع احيانا شيئا ما من هذه الغشاوة فنرى امرا كان امامنا طوال الوقت  ولكنه كان فى نفس الوقت مستورا عنا. وبهذه الروح نتناول موضوع اليوم الخاص بظاهرة دوبلر.

وظاهرة دوبلر هي اكتشاف قديم. ويعودالفضل فى اكتشافها الى فلكى وفيزيائى نمساوي يدعى دوبلر فى القرن التاسع عشر. زمع ذلك  فللظاهرة تطبيقاتها الهائلة فى حياتنا اليوم. وبالرغم من  ان هذه الظاهرة تنتمى الى ميدان الفيزياء الكلاسيكية الا ان لها ايضا دورها المهم فى  ميدان الفيزياء الحديثة وخاصة ميدان الكوزمولجى. وظاهرة دوبلر توضح تأثير الحركة على الاحساس بتردد بالموجات. ويمكننا تلخيص امر هذه الظاهرة فى الخلاصة التالية: اذا كان مستقبل الموجات فى حالة حركة نسبية باتجاه مصدرها فانه يشعر بان لها تردد اعلى من حقيقتها. والعكس صحيح فاذا كان مستقبل الموجات يتحرك مبتعدا عن الموجات او مصدر الموجات يتحرك مبتعدا عن المستقبل فتبدو هذه الموجات بالنسبة لمستقبلها وكأنها ذات تردد اقل.

والان لنأتى للتفاصيل. ولنرى اولا حالة ان المستقبل ثابت بينما مصدرالموجات متحرك:

بطة تسبح وظاهرة دوبلر

ولنبدأ بمثال من الموجات الموئية. فالموجات المائية تتمتع بميزة هامة وهى اننا نستطيع ان نرى الموجات بشكلها النمطى امام اعيننا. فعندما نلقى بحجر فى الماء تتكون موجات مائية عبارة عن دوائر متداخلة ومتحدة المركز. وهذا الشكل نعرفه كلنا جيدا. لكن ماذا يحدث عندما يكون مصدر الموجات متحرك؟. فماذا مثلا سوف يكون شكل الموجات المائية عندما تسبح بطة باتجاه اليمين كما بالصورة ؟  ستكون الموجات عبارة عن دوائر متداخلة ولكنها لن تكون متحدة المركز لان مركز الموجات يسبح باتجاه اليمين! ولذلك فستبدو الموجات بالنسبة لمستقبل يوجد على يمين البطة وكأنها ذات طول موجى اقصر وبالتالى تردد اعلى. حيث ان الطول الموجى والتردد هما صفتان عكسيتان. وتبدو الموجات بالنسبة لراصد على يسار البطة بطول موجى اطول وبالتالى تردد اقل. واذا حذفنا  البطة من الصورة  باستخدام برنامج كالفوتوشوب وتركنا الموجات على حالها فسوف نستطيع مع ذلك ان ان ندرك فورا ان مصدر الموجات يتحرك باتجاه اليمين. هذا المثال البسيط يجسد ظاهرة دوبلر.  وهذا هو كل شئ!

مثال اخر اذا استتبدلنا الموجات المائية بموجات ضوئية فسنصل الى نتيجة مشابهة تماما. فمصدر ضوئى يتحرك باتجاهنا سوف يبدو لنا بطول موجى اقل وبالتالى بتردد اعلى وبيدو لنا وكأن طيفه الضوئى منزاح نحو اللون الازرق حيث هو الاعلى ترددا فى الالوان. بينما مصدر ضوئى يتحرك بعيدا عنا سيظهر لنا بطول موجى اطول وبتردد اقل وسيبدو طيفه منزاحا باتجاه اللون الاحمر وهو الاقل ترددا فى الالوان. وهذه هى عين الظاهرة اللتى استغلها هبل فى اكتشاف ان المجرات  تتباعد عنا. وان الكون فى حالة اتساع مستمر. وهذه من اهم الادلة على صحة نظرية الانفجار العظيم big bang

طائرة تخترق جدار الصوت

مثال اخر من عالم الموجات الصوتية: فاذا استبدلنا البطة فى الصورة بطائرة تطير بسرعة الصوت. فسنجد ان الموجات ستنزاح باتجاه حركة الطائرة كما فى حالة البطة تماما. لكن فى هذه الحالة فان مقدمات الموجات ستتماس كلها فى نقطة واحدة وتشكل ما يشبه حائطا مضغوطا او جدارا. وهذا ما يطلق عليه مجازا جدار الصوت.  واذا طارت الطائرة بسرعة اعلى من سرعة الصوت فعليها ان تخترق هذا الجدار كما فى الصورة. مما ينشأ عنه صوت فرقعة مدوية.

زلزال سان فرانسيسكو

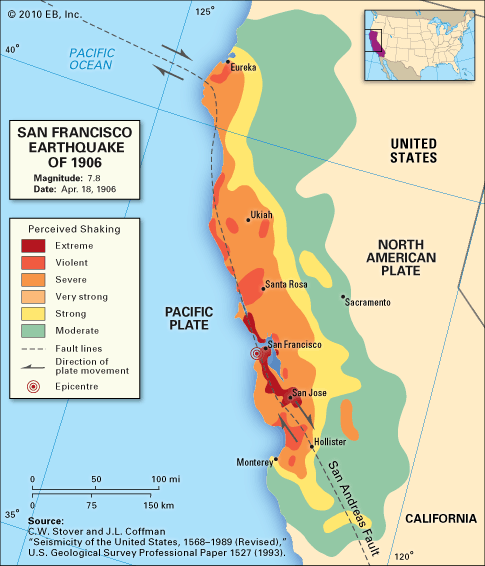
مثال رابع من ميدان مختلف وهو ميدان الزلازل. فى زلزال سان فرانسيسكو عام 1906 كانت الخسائر فى مدينة سانتا روزا اعلى منها فى مدينة سان جوزيه بالرغم من ان المدينة الثانية كانت اقرب الى قلب الزلزال. والتفسير يرجع مرة اخرى فى ظاهرة دوبلر. فالسبب التقليدي للزلازل السطحية هو كسر ما يحدث بداخل طبقة الارض. وفى حالة زلزال سان فرانسيسكو كان الكسر عن طريق قوي القص. اى ان صفائح الارض تنزلج امام بعضها على امتداد صدع سان اندرياس الموجود بالصورة. وفى المثال السابق ابتدأ الكسر  بالقرب من سان جوزيه ولكنه توسع وانتشر باتجاه سانتا روزا . تماما كما السحاب او السوستة الموجود فى الملابس عندما نفتحه. اذن فالمدن اللتى تقع باتجاه انتشار الكسر الارضى تشعر بالزلزال بتردد وبطاقة اعلى منه من المدن اللتى تقع فى الجهة العكسية منه. ومن حسن الحظ ان سرعة انتشار الكسر الارضى فى باطن الارض اقل من سرعة انتشار الموجات الزلزالية فوق سطح الارض . والا كنا سنحصل على حالة كحالة الطائرة اللتى تخرق جدار الصوت وستكون النتائج اكثر كارثية.

مثال اخر من ميدان مختلف. فى سباقات السيارات الفورمولا 1 نسمع للسيارات صوتا مميزا. او حتى عندما نقف على طريق السفر السريع نستمع الى صوت السيارات العابرة فنسمع هذا الصوت المميز. ولا اعنى هنا شدة الصوت. فبالطبع كلما تكون السيارة اقرب منا تكون شدة الصوت اعلى. لكننى اقصد نغمة الصوت.  سنجد ان للسيرات نغمة مميزة قد تبدو هكذا iiiiuuuu . لكن ما هو السبب فى تغيير نغمة الصوت؟ فحال السيارة يبقى كما هو. السبب هو ظاهرة دوبلر. فعندما تقترب منا السيارة بسرعة عالية يكون تردد الصوت اعلى من حقيقته وعندما  تبتعد عنا يكون  تردد الصوت اقل!

الان سنحاول ان نجد الصياغة الرياضية لظاهرة دوبلر. وهذه عملية سهلة عكس ما قد يتوقع البعض. ونحتاج فقط الى معرفة قاونين يربطان خواص الموجات. القانون الاول يقول ان الزمن الدوري او زمن اهتزازة واحدة هو مقلوب التردد أو

T = 1/f        1

اما القانون الثانى فيربط بين سرعة انتشار الموجات c والتردد f والطول الموجى L ونلاحظ العلاقة العكسية السابق ذكرها بين التردد والطول الموجى فاحدهم يقع فى البسط والاخر فى المقام. فعندما يكون احدهما كبيرا يكون الاخر صغيرا:

f= c/L      2

اذن فى الحالة العادية  سيكون الطول الموجى طيقا اللقانون الثانى
L = c/f

ولكن حيث ان مصدر الموجات يتحرك. ففى زمن دورة واحدة  T  سيتحرك مصدر الموجات بالسرعة v اذن سيكون الطول الموجى بالنسبة لمستقبل يقع باتجاه انتشار الموجة اقل. وهنا ساتستخدم الرمز R للتعبير عن المستقبل او Reciever

L(R) = c/f – v/f

مع ملاحظة  ان سرعة الموجات ستبقى بالنسبة للمستقبل ثابتة. فسوف تصل الموجة الاولى فى وقتها تماما سواء تحرك المصدر ام لا. فقط اذا تحرك المصدر ستصل الموجات التالية بشكل اسرع. ولكن هذا سوف يفسره المستقبل بان الطول الموجى يقل. اذن بالتعويض فى القانون الثانى نحصل على:
f(R) = f/(1-v/c)       3

واذا كان مصدر الموجة يتحرك مبتعدا عن المستقبل سيكون التردد من وجهة نظر المستقبل كالتالى:
f(R) = f/(1 + v/c)     4

الان سننتقل الى الحالة الثانية عندما يكون مصدر الموجة ثابتا ولكن المستقبل هو اللذي يتحرك:

وهنا قد يتعجب البعض.  الن تكون النتيجة نفسها كما لو كان مصدر الموجة هو المتحرك؟ اليس هذا هو جوهر النظرية النسبية لاينشتاين؟ فلا توجد حركات مطلقة. فكل الحركات نسبية . فحتى لو كان المستقبل  للموجة متحركا. افليس بامكاننا تخيله ثابتا واعتبار مصدر الموجات هو المتحرك فى الاتجاه المعاكس ثم نحصل على نفس النتيجة الاصلية بدون ادنى تغيير؟ هذا سؤال جيد ولكننا سوف نرجئ الاجابة عليه الان. وسنعود له لاحقا. لكن من وجهة النظر الاخرى دعونا نتخيل الاتى: لو كان مستقبل الموجات يتحرك بسرعة الصوت مبتعدا عن مصدر صوتى فان الصوت لن يصل اليه وسيبدو ان التردد صفر. لكن اذا كان المستقبل ثابتا ومصدر الصوت هو اللذي يبتعد بسرعة الصوت فان الصوت سوف يصل.  صحيح بنصف التردد ولكنه سوف يصل. لماذا؟ لاننا اغفلنا شيئا مهما فى هذا الموضوع حتى الان وهو  الهواء او وسط انتقال الصوت. فيمكننا تشبيه الموقف بسباق  التتابع فى العاب القوي.  حيث يتناوب 4 عدائين على تناول عصا فيما بينهم حتى نهاية السباق. فمصدرالاشارة الصوتية  هو العداء الاول و المستقبل هو العداء الثالث. اما العداء الثانى فهو الهواء. وهو شئ لانراه ولكنه موجود وبمجرد ان يستلم عصا التتابع من العداء الاول يقوم دائما بتسليمها بنفس السرعة c . صحيح ان المسافة تتباعد دائما بين العدائين الاول و الثالث لكن طالما تسلم العداء الثانى الاشارة الصوتية من العداء الاول فانه يقوم بعملية التسليم!!

ودعونا نرى الصياغة الرياضية. فى هذه المرة ستبقى شكل الموجات على هيئة دوائر متحدة المركز. فالمستقبل هو اللذى يتحكر باتجاهها بالسرعة v

اذن الطول الموجى بالنسبة للمستقبل سييقى كما هو
L = c/f

لكن من ناحية اخرى سيشعر المستقبل ان الموجة الاولى سوف تصل اليه سريعا بفعل حركته هو. او ان
c(R) = c + v
مرة اخرى بالتعويض فى المعادلة 2 نحصل على
f(R) = f(1 +v/c)      5
اما اذا كان المستقبل متحركا مبتعدا عن المصدر فسيكون التردد
f(R) = f(1 – v/c)    6

وهنا تجدر الملاحظة بانه اذا كانت سرعة الحركة النسبية  صغيرة بالنسبة لسرعة انتشار الموجة. كما فى حالة الموجات الضوئية. حيث ان سرعة الضوء هى اعلى السرعات الموجودة فى الكون  تتحول الحالتان السابقتان الى حالة واحدة فرقميا وبشكل تقريبى  نحصل على
1+0.1 = 1.1 = 1/(1-0.1) = 1.1111

دعونا الان نرى تطبيقا عمليا للنقطة السابقة وهو جهاز الرادار اللتى تستخدمه الشرطة فى رصد السيارات المسرعة. فهذا الجهاز مبنى على ظاهرة دوبلر. فالجهاز هو مصدر موجات كهرومغناطيسية ذات تردد ثابت. وعندما تقترب سيارة مسرعة من الجهاز. تبدو لها هذه الموجات كما سبق بتردد اعلى. وتقوم السيارة المسرعة بعكس هذه الموجات مرة اخرى باتجاه جهاز الردار. وهنا سوف يلاحظ الجهاز الفارق بين الموجات الصادرة والموجات المرتدة وعن طريق حساب الفارق يستطيع تحديد سرعة السيارة بدقة وان كانت تجاوزت السرعة المسموحة اما لا!!

فى النهاية نعود الى اصدقاء النظرة النسبية ونجاوب على السؤال تعارض ظاهرة دوبلر مع النظرية النسبية. افلن نستطيع ان نتعرف على حركتنا المطلقة مثلا عن طريق التجربة الذهنية التالية؟: نتخيل ان لدينا الة نفخ ذات نغمة معينة نعرفها جيدا ثم نعطيها لانسان ونطلب منه ان يعزف على هذه الالة. فى هذه الاثناء نركب دراجة وننتحرك بها بسرعة الصوت باتجاه مصدر الصوت. وحيث ان اذننا موسيقية سنسمع النغمة ذات صوت مختلف وان لها تردد اعلى ويساوي ضعف ترددها الاصلي. وهنا سوف ندرك اننا فى حالة حركة مطلقة بسرعة الصوت باتجاه مصدر الصوت!! . لكن هذا التحليل غير سليم فهنا قد اهملنا دور الهواء وهو مرة اخرى العداء الثانى فى سباق التتابع! فنحن بامكاننا تخيل المشهد على الصورة التالية عندما نضغط على دواسات الدراجة تتحرك الكرة الارضية كلها بما تحمل تحت دراجتنا . فسيقترب منا الزامر بسرعة الصوت. كما سيتحرك الهواء باتجاهنا . ودليلنا هو ذلك الشعور اللذى سوف نشعر به عندم يلفح الهواء وجهنا وجسمنا من الامام ويضغطهما بقوة كبيرة. اذن نحن ثابتون ويتحرك الصوت فى الهوء بسرعة c ثم يتحرك الهواء كله باتجاهنا بالسرعة c . وحيث ان المسافة الموجية ثابتة فسيظهر لنا الصوت بضعف التردد!! مرة اخرى النظرية النسبية تنتصر.

لكن ما غيرته النظرية النسبية فى قانون دوبلر كما فعلت فى قوانين كثيرة اخرى. هى انها غيرت صورته الرياضية ولكن ليس فى جوهره. فعند جمعنا للسرعات لايمكننا ان نجمعها حسابيا كما فعلنا فى اشتقاقنا السابق . كما ان علينا ان نراعى ان الزمن والطول هى مقادير نسبية مختلفة حسب الناظر لها. وظاهرة دوبلر الموافقة للنظرية النسبية تبقى فى  الجوهر كما هي ولكنها تحمل  فقط صياغة رياضية مختلفة بعض الشئ.