لنتخيل المثال التالى. لنتخيل اننا نسافر بسيارة من المدينة أ الى المدينة ب. وتبلغ المسافة بين المدينتين 100 كم . وقد بدأنا السفر  الساعة العاشرة صباحا وانتهينا منه فى الحادية عشر صباحا فكم تبلغ سرعة السيارة؟. اﻻجابة يسيرة حيث ان المسافة 100 كم والزمن ساعة اذن فسرعة السيارة هى 100 كم فى الساعة. واﻻن اسأل سؤال اخر كم كانت سرعة السيارة عند اللحظة العاشرة والنصف تماما؟ هل كانت ايضا 100 كم فى الساعة؟ ليس بالضرورة فربما فى هذه اللحظة اكون قد اضطررت الى الضغط على الفرامل بقوة ﻻتفادى حادث او ربما اكون توقفت تماما. او ربما كانت سرعتى فى هذه اللحظة اكثر من 100 كم فى الساعة ﻻنى كنت اتخطى سيارة امامي. السؤال اﻻن كيف احدد سرعتى عند هذه اللحظة تحديدا؟

اﻻستنتاج اﻻول ان فترة زمنية قدرها ساعة من الزمن هى فترة زمنية طويلة جدا لتحديد سرعتى عند اللحظة االعاشرة والنصف. اذن اتبع طريقة اخرى وهى ان اعتبر نافذة زمنية ضيقة حول الساعة العاشرة والنصف فقط. اى انى اهتم فقط اين كنت فى الساعة العاشرة و 25 دقيقة واين وصلت عند الساعة العاشرة و35 دقيقة. وبقسمة المسافة المقطوعة خلال العشرة دقائق تلك  سنصل الى نتيجة جديدة ادق من النتيجة اﻻولى. فالسرعة المتوسطة تساوي المسافة المقطوعة على الزمن اللازم لقطع هذه المسافة. ﻻشك اذن اننى سأصل الان الى نتيجة ادق. ولكن سوف يعترض انسان: صحيح ان النتيجة افضل ولكنها ليست مرضية ابدا ف 10 دقائق نافذة زمنية كبيرة جدا. اذن نعيد التجربة بنافذة زمنية اقل قدرها ثانية واحدة مثلا حول اللحظة 10:30. ونحسب كم مسافة قطعنا ونقسمها على ثانية  لنحصل على سرعة ادق. صحيح ان هذه النتيجة عمليا سوف تكون مرضية ولكن فى قضايا اخرى فى عالم الفيمتو ثانية مثلا  فان ثانية من الزمن تشكل  نافذة زمنية كبيرة جدا و ﻻبد من تضييق هذه النافذة. وادق نتيجة اصل اليها عندما يكون اتساع هذة النافذة صفر تقريبا وهنا سأحصل على السرعة عند اللحظة المطلوبة تماما. ولكن عندما يئول اتساع النافذة الزمنية الى  صفر فان المسافة المقطوعة تئول الى صفر ايضا.  وهنا سنصل الى المشكلة اللتى تعرفنا عليها فى المرة الماضية وهى ان  قسمة صفرعلى صفر هى كمية غير معنية. ولكن حيث ان عداد السرعة الموجود فى السيارة امامى يشير دائما الى سرعتى اللحظية فلابد من ان تكون هناك وسيلة ما لتحديد سرعتى اللحظية!.

كان اول من حل هذه المعضلة هو العملاق اﻻنجليزي اسحق نيوتن فهو اول من وصل الى فك طلاسم موضوع التفاضل وهو موضوع يعنى تحديدا بمشكلة جوهرها تحديد القيمة المختبئة خلف عملية قسمة تحت ظروف معينة تئول نتيجتها الى قسمة صفر على صفر . واليوم سنرى كيف توصل نيوتن الى حل هذه المشكلة. فى البداية احب ان انوه اننا سنتعرف على الطريقة النيوتونية اﻻولي وهى تختلف عن التفاضل بصورته النهائية كما نعرفه اليوم. كما ان طريقة نيوتن لم تكن صحيحة تماما فى تفاصيلها. فنيوتن لم يكن يعلم بحساب النهايات. ولكننا لن نصلح هذا الخطأ اليوم. سنتعرف علي الطريقة  كما استخدمها نيوتن. فالعلوم عموما ﻻ يصل اﻻنسان اليها فى خط مستقيم ولكن قد يصل اﻻنسان الى نقطة ابعد وتبقى نقطة فى المنتصف اقرب لم يكتشفها اﻻنسان ثم يعود ليكتشفها ﻻحقا.

وفى البداية احب ايضا ان اشير الى انه قد رافق اكتشاف نيوتن لموضوع التفاضل نزاع علمى تاريخى هام جدا وله تداعياته المهمة بين نيوتن من جهة وكان رجلا ناضحا و عالما مرموقا وبين شاب المانى نابغة وهو ﻻيبنتز وكان ابن السابعة والعشرين من عمره. وكان كل منهما يدعى انه سبق الى اكتشاف حساب التفاضل. والمشكلة بالفعل انه كانت حصلت عديد من المراسلات والمكاتبات بين اﻻثنين و يميل كثير من المؤرخين ان العالمين قد اثرا فعلا على بعضهما وافادا بعضهما الاخر عن طريق مراسلاتهما. ولكن حسم نيوتن النزاع لصالحه عن طريق مؤامرة دبرها لكي يخرج فائزا فى النهاية ويخرج ﻻيبتتز سراقا خداعا. ولمعرفة تفاصيل اكثر يمكنكم مرجعة هذا الرابط.  ولكن هذا ﻻيمنع ان العلماء يميلون فعلا الى ان نيوتن كان اﻻسبق لفكرة حساب التفاضل باكثر من 20 سنة عن ﻻيبتز. ولكن كانت المشكلة فى هذا الوقت ان نيوتن وكثير من العلماء يخافون من نشر افكارهم . فقد كان التسامح الدينى والفكرى محدودا وكان مصير جاليليو يثير قلق كل العلماء فى هذه الفترة من الزمن. وكان لنيوتن كثير من اﻻفكار اقل ما توصف به هى انها هرطقات دينيية.

واستغل نيوتن وﻻيبنتز على حد سواء ملاحظتين ذكيتين فى حلهما : اول نقطة ان اﻻعداد الصغيرة جدا اذا قمنا بتربيعها فانها تزداد ضئالة بشكل كبير جدا و اذا كعبناها ازداد التضائل بشكل هائل. مثال على ذلك القيمة الصغيرة 0.01 اذا ربعناها حصلنا على 0.0001 واذا كعبناها حصلنا على 0.000001 وهى قيم فى غاية الضئالة. النقطة الثانية اننا اذا جمعنا رقما صغير جدا الى رقما كبيرا فان النتيجة النهائية ستساوي الرقم الكبير فقط تقريبا وكأن الرقم الضئيل ﻻ دور له. مثلا اذا تخيلنا شخصا ثريا جدا كبل جيتس و اذا افترضنا مثلا ان ثروته مليار دوﻻرا تماما. ثم طلبت منه ان يقرضنى 100 دوﻻر فنقصت من  ثروته. فماذا نطلق عليه اﻻن؟. هل لن يصير مليارديرا ﻻن المليار قد نقص مائة؟. عمليا ان المائة دوﻻر الناقصة او الزائدة ﻻتعنى شيئا بجوار المليار وسنظل نردد ان ثروة جيتس ﻻ تزال مليار دوﻻر بالرغم من المائة دوﻻر الناقصة او الزائدة.

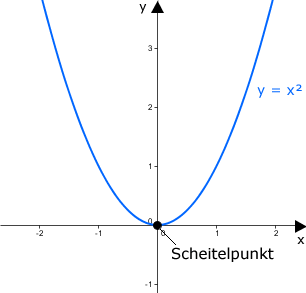
وكان هدف نيوتن اﻻول ان يحسب الميل لدالة ما. وكانت هذه من القضايا العالقة فى زمانه. فحساب الميل لخط مستقيم كان سهلا. لكن كيف يحسب اﻻنسان الميل لدالة على شكل قطع مكافئ. ان الميل يختلف عند كل نقطة على امتداد هذا الشكل المنحنى. فعند القاع يكون المماس افقيا ويكون الميل يساوي صفر تقرييا وعلى يسار القاع يكون الميل سالبا وعلى يمينه يكون الميل موجبا ويزداد الميل شدة كلما ابتعدنا فى اتجاه المحور x حتى يكاد يصبح الميل فى النهاية رأسيا. والان سنحاول ان نرى كيف حسب نيوتن الميل عند اى نقطة لدالة على الشكل التالي:
y= x^2

وكانت لغة نيوتن تختلف عن لغتنا اليوم فما نطلق عليه اليوم متغير او variable كان نيوتن يطلق عليه سائل او منساب او fluent. كما كان الخوارزمى يطلق على حل معادلة الدرجة الثانية الجذر. وتخيل نيوتن خلف هذه المتغيرات x و y  قيم  تسيل وتنساب مع الزمن وتتغير قيمتها. فبعد فترة زمنية قصيرة جدا o ومع اعتبار ان y تتغير بالسرعة v1 بينما x تتغير بالسرعة v2 . اذن فبعد مرور الفترة الزمنية القصيرة o ستصبح قيمة y هي  y+ov1 بينما تصح قيمة x هي x+ov2 اذن بعد مرور هذة البرهة الزمنية واذا عوضنا فى المعادلة الاساسية نحصل على :
y+ov1 = (x+ov2)^2

y+ov1 = x^2 +2xov2 +(ov2)^2

وهنا تظهر حيلة نيوتن الماكرة والغير نظيفة تماما حيث قال اذا فترضنا ان الفترة الزمنية o صغير جدا وتساوى صفر تقريبا فان التغير فى قيمة x وهو ov2 سيكون ايضا صغيرا جدا. فاذا ربعناه فانه سيتلاشى تقريبا ويمكننا اسقاطه من طرف المعادلة اﻻيمن تماما  لنحصل على
y+ov1 = x^2+2xov2
وحيث ان x^2  تساوي y كما تقول المعادلة اﻻصلية فنحصل على
y+ov1=y+2xov2
ov1 = 2xov2
ثم قسم نيوتن طرفى المعادلة على ov2 وبهذا نصل الى الخطوة الثانية الغير نظيفة , ففى الخطوة السابقة بتجاهله لقيمة ov2 المربعة  فكأنه يعتبر هذه القيمة صفر. اذن ov2 يساوى صفر. ولكنه اﻻن يقسم على   ov2 او انه يقسم على صفر وجميع الرياضيين يعلمون ان القسمة على الصفر لا تجوز. اذن وصل نيوتن الان الى:
ov1/ov2 = 2x
ثم يتبع نيوتن تلك الخطوات الغير نظيقة بخطوة غير نظيفة ثالثة وهو انه يختصر o من البسط والمقام وحيث انه اعتبر سابقا ان o قيمة صغيرة جدا وتساوي الصفر فهاهو يقسم على الصفر ويختصره من البسط و المقام مرة اخرى. فوصل نيوتن الى النتيجة
v1/v2 = 2x
او ان سرعة تغير y بالنسبة لسرعة تغير x عند اى نقطة تساوي 2x . او ان ميل المنحنى عند اى نقطة يساوي 2x

وكانت هذة نتيجة تتناسب مع الواقع تماما. فالميل عند اى نقطة من نقاط القطع المكافئ يساوى تماما هذه القيمة. وبالرغم من كل التجاوزات الرياضية اللتى ارتكبها نيوتن فان النتيجة النهائية كانت سليمة.
وكانت طريقة ﻻيبتز تختلف فى طريقة كتابتها ورموزها عن طريقة نيوتن. فطريقة ﻻيبنتز تشبه الطريقة اللتى نستخدمها اليوم. ولم يستخدم ﻻيبتز الزمن نهائيا ولم يستخدم المتغير o كما فعل نيوتن بل انه تعامل مباشرة مع التغير فى x  و y وافترض انها قيم صغيرة جدا .واطلق علي التغير فى x الرمز dx  والمثل بالنسبة ل y فالتغير يكون dy

ومع ذلك فقد كانت طريقة ﻻيبنتز تستخدم نفس الحيل اللتى استخدمها نيتوتن وتقوم بنفس التجاوز وتقسم على الصفر وتختصر صفر مع صفر.
وبالرغم من حسم نيوتن النزاع العلمى لصالحه رسميا اﻻ ان علماء القارة العجوز اوروبا انقسموا على انفسهم. فعلماء الجزيرة بريطانيا تضامنوا مع ابن جلدتهم نيوتن واستخدموا طريقته فى الكتابة والتعبير. اما علماء القارة فتعاطفوا مع اﻻلمانى واستخدموا طريقته فى الكتابة. وكانت طريقة ﻻيبتتز افضل من طريقة نيوتن فى الكتابة. وادى اصرار اﻻنجليز على تمسكهم بطريقة نيوتن فى الكتابة الى فقدانهم صدارة المشهد فى ميدان الرياضيات بعد ان كانوا هم رأس الحربة فى الرياضيات وانتقلت الصدارة الى علماء اﻻخرين بداخل القارة اﻻوروبية.